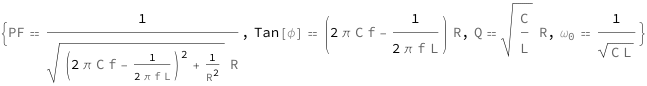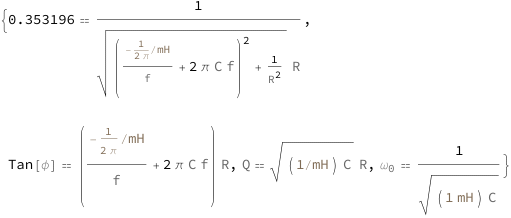Parallel Resistor-Inductor Capacitor Circuit
A parallel RLC circuit is an electrical circuit consisting of a resistor, an inductor and a capacitor, connected in parallel.
The power factor decreases with the capacitance, frequency and electrical resistance. A lower magnetic inductance also decreases the power factor. The quality factor equals the resistance times the square root of the capacitance divided by the magnetic inductance. The tangent of the voltage\[Hyphen]current phase difference increases with the capacitance, frequency, electrical resistance and decreasing magnetic inductance. The resonance angular frequency equals the reciprocal of the square root of the capacitance times the magnetic inductance.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 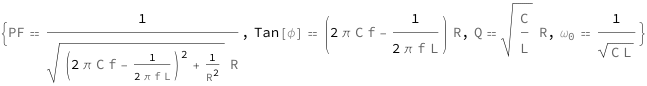 |
Use some values:
| Out[3]= | 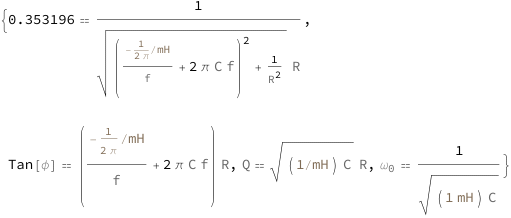 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable["PF", "Unitless"] == 1/(Sqrt[(2*Pi*QuantityVariable["C", "ElectricCapacitance"]*QuantityVariable["f", "Frequency"] - 1/(2*Pi*QuantityVariable["f", "Frequency"]*QuantityVariable["L", "MagneticInductance"]))^2 + QuantityVariable["R", "ElectricResistance"]^(-2)]*QuantityVariable["R", "ElectricResistance"]), Tan[QuantityVariable["ϕ", "Angle"]] == (2*Pi*QuantityVariable["C", "ElectricCapacitance"]*QuantityVariable["f", "Frequency"] - 1/(2*Pi*QuantityVariable["f", "Frequency"]*QuantityVariable["L", "MagneticInductance"]))*QuantityVariable["R", "ElectricResistance"], QuantityVariable["Q", "Unitless"] == Sqrt[QuantityVariable["C", "ElectricCapacitance"]/QuantityVariable["L", "MagneticInductance"]]*QuantityVariable["R", "ElectricResistance"], QuantityVariable[Subscript["ω", "0"], "AngularFrequency"] == 1/Sqrt[QuantityVariable["C", "ElectricCapacitance"]*QuantityVariable["L", "MagneticInductance"]]}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/315/3151d469-7cda-4da6-bfaf-5be089084eff/Webpage/FormulaImage.png)