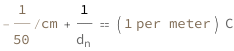Corrective Lens Equation for Farsightedness
The corrective lens equation for farsightedness relates the comfortable reading distance for a person to the necessary lens power to correct it.
The difference between the reciprocals of the comfortable reading distance in normal vision and the shortest distance at which a farsighted person can read without glasses is directly proportional to the lens power or the spherical component of a lens prescription.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= |  |
Use some values:
| Out[3]= | 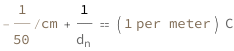 |
External Links
Publisher Information
![Copy to Clipboard -QuantityVariable[Subscript["d", "min"], "Distance"]^(-1) + QuantityVariable[Subscript["d", "n"], "Distance"]^(-1) == Quantity[1, "Meters"^(-1)]*QuantityVariable["C", "OpticalPower"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/2a6/2a65aebf-6134-44dc-97eb-816c9f3f0ae4/Webpage/FormulaImage.png)