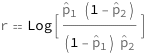Log Odds Ratio
The log odds ratio is a way to quantify how strongly the presence or absence of property A is associated with the presence or absence of property B in a given population.
The log odds ratio equals the logarithm of the ratio of the product of the first sample proportion and 1 minus the second sample proportion and the product of the second sample proportion and 1 minus the first sample proportion.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 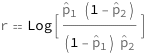 |
Use some values:
| Out[3]= | 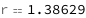 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["r", "Unitless"] == Log[(QuantityVariable[Subscript[OverHat["p"], "1"], "Unitless"]*(1 - QuantityVariable[Subscript[OverHat["p"], "2"], "Unitless"]))/((1 - QuantityVariable[Subscript[OverHat["p"], "1"], "Unitless"])*QuantityVariable[Subscript[OverHat["p"], "2"], "Unitless"])]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/27c/27c53d83-4356-4ee0-a74b-10f18ddfb93d/Webpage/FormulaImage.png)