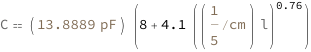Self-Capacitance of a Solid Cylinder
Self-capacitance is the amount of electric charge that must be added to an isolated conductor to raise its electric potential by one unit.
The self-capacitance of a solid cylinder is directly proportional to the electric permittivity of the insulator. The self-capacitance increases with the radius of the cylinder to the 0.24 power and the length of the cylinder to the 0.76 power.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 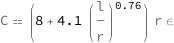 |
Use some values:
| Out[3]= | 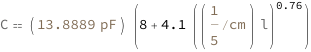 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["C", "ElectricCapacitance"] == (8 + 4.1*(QuantityVariable["l", "Length"]/QuantityVariable["r", "Radius"])^0.76)*QuantityVariable["r", "Radius"]*QuantityVariable["ε", "ElectricPermittivity"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/269/269048ca-a188-4718-bb45-dd534ee42b74/Webpage/FormulaImage.png)

![FormulaData[
ResourceObject[
"Self-Capacitance of a Solid Cylinder"], {QuantityVariable[
"\[Epsilon]","ElectricPermittivity"] ->
Quantity[277.778`, ("Picofarads")/("Meters")],
QuantityVariable["r","Radius"] -> Quantity[5, "Centimeters"]}]](images/269/269048ca-a188-4718-bb45-dd534ee42b74-io-3-i.en.gif)