Fabry–Pérot Interferometer Using Finesse Coefficient
This formula describes the transmission and reflection of light through a FabryPérot interferometer, or etalon, a transparent plate with two reflecting surfaces or two parallel, highly reflecting mirrors.
Interferometer transmittance decreases with increasing values of the finesse coefficient, and varies inversely with the sine of the product of the plate spacing, the index of refraction, the reciprocal of the wavelength and the cosine of the angle of incidence. Interferometer reflectance is 1 minus the transmittance.
Formula
![Copy to Clipboard {QuantityVariable[Subscript["T", "e"], "Unitless"] == (1 + QuantityVariable["ℱ", "Unitless"]*Sin[(2*Pi*Cos[QuantityVariable["θ", "Angle"]]*QuantityVariable["l", "Distance"]*QuantityVariable["n", "Unitless"])/QuantityVariable["λ", "Wavelength"]]^2)^(-1), QuantityVariable[Subscript["R", "e"], "Unitless"] == 1 - QuantityVariable[Subscript["T", "e"], "Unitless"]}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/263/2639d2be-9f5a-4efc-b6fd-0db0dfd9b8fd/Webpage/FormulaImage.png)
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 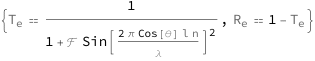 |
Use some values:
| In[3]:= |
| Out[3]= | 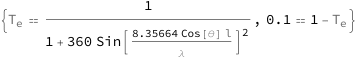 |