Wolfram Computation Meets Knowledge

Wolfram Formula Repository (Under Development)

Law of Haversines

The haversine formula determines the great-circle distance between two points on a sphere given their longitudes and latitudes.

The haversine of the angular length of the third side equals the haversine of the difference between the angular lengths of the first and second sides plus the product of the haversine of the angle opposite the third side, the sine of the angular length of the first sides and the sine of the angular length of the first sides.

Formula

Haversine[QuantityVariable["c", "Angle"]] == Haversine[QuantityVariable["a", "Angle"] - QuantityVariable["b", "Angle"]] + Haversine[QuantityVariable["γ", "Angle"]]*Sin[QuantityVariable["a", "Angle"]]*Sin[QuantityVariable["b", "Angle"]]

symbol description physical quantity
c third side angular length "Angle"
a first side angular length "Angle"
b second side angular length "Angle"
γ angle opposite third side "Angle"

Forms

Examples

Get the resource:

In[1]:=
ResourceObject["Law of Haversines"]
Out[1]=

Get the formula:

In[2]:=
FormulaData[ResourceObject["Law of Haversines"]]
Out[2]=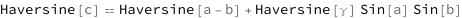

Use some values:

In[3]:=
FormulaData[ ResourceObject[ "Law of Haversines"], {QuantityVariable["\[Gamma]","Angle"] -> Quantity[\[Pi]/2, "Radians"], QuantityVariable["a","Angle"] -> Quantity[\[Pi]/2, "Radians"]}]
Out[3]=

Source Metadata

  • Creator:
  • Date: 1805

Publisher Information