Hypsometric Equation
The hypsometric equation, also known as the thickness equation, relates an atmospheric pressure ratio to the equivalent thickness of an atmospheric layer under the assumptions of constant temperature and gravity.
The final pressure equals the reference pressure times an exponential that decreases as the difference between the altitudes of the final and reference pressures divided by the reference temperature grows.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 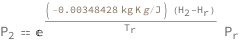 |
Use some values:
| Out[3]= | 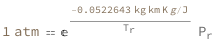 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable[Subscript["P", "2"], "Pressure"] == E^((Quantity[-0.0034842841364027557, ("Kelvins"*"Kilograms"*"StandardAccelerationOfGravity")/"Joules"]*(QuantityVariable[Subscript["H", "2"], "Height"] - QuantityVariable[Subscript["H", "r"], "Height"]))/QuantityVariable[Subscript["T", "r"], "Temperature"])*QuantityVariable[Subscript["P", "r"], "Pressure"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/20c/20c81207-70ec-412e-b3dc-c18e4ee4fc25/Webpage/FormulaImage.png)
