Relativistic de Broglie Angular Frequency by Velocity
The de Broglie angular frequency is the angular frequency associated with a massive particle in motion according to quantum mechanics, accounting for relativistic effects.
The de Broglie angular frequency is proportional to the mass divided by the square root of 1 minus the square of the ratio between the velocity and the speed of light.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 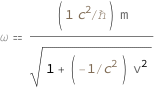 |
Use some values:
| Out[3]= | 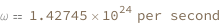 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["ω", "AngularFrequency"] == (Quantity[1, "SpeedOfLight"^2/"ReducedPlanckConstant"]*QuantityVariable["m", "Mass"])/Sqrt[1 + Quantity[-1, "SpeedOfLight"^(-2)]*QuantityVariable["v", "Speed"]^2]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/1fe/1fef144e-2b1d-42db-9630-85bec9d55132/Webpage/FormulaImage.png)

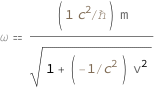
![FormulaData[
ResourceObject[
"Relativistic de Broglie Angular Frequency by Velocity"], \
{QuantityVariable["m","Mass"] -> Quantity[1.`, "NeutronMass"],
QuantityVariable["v","Speed"] ->
Quantity[1, ("Meters")/("Seconds")]}]](images/1fe/1fef144e-2b1d-42db-9630-85bec9d55132-io-3-i.en.gif)