Area Moment of Inertia of a Regular Pentagon about a Centroidal Axis
The second moment of area, also known as moment of inertia of plane area, area moment of inertia or second area moment, is a geometrical property of an area that reflects how its points are distributed with regard to an arbitrary axis.
The second moment of area for a regular pentagon equals edge length to the fourth power multiplied by a constant.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 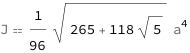 |
Use some values:
| Out[3]= | 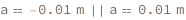 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["J", "SecondMomentOfArea"] == (Sqrt[265 + 118*Sqrt[5]]*QuantityVariable["a", "Length"]^4)/96](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/1ee/1ee42d7f-cd73-491f-9eec-06e68ebf8b23/Webpage/FormulaImage.png)

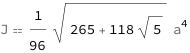
![FormulaData[
ResourceObject[
"Area Moment of Inertia of a Regular Pentagon about a Centroidal \
Axis"], {QuantityVariable["J","SecondMomentOfArea"] ->
Quantity[0.239551`, ("Centimeters")^4]}]](images/1ee/1ee42d7f-cd73-491f-9eec-06e68ebf8b23-io-3-i.en.gif)