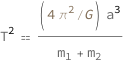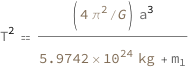Kepler's Third Law
Kepler's laws of planetary motion are three scientific laws describing the motion of planets around the Sun. The third law states that the square of the orbital period of a planet is proportional to the cube of the semimajor axis of its orbit.
The orbital period squared increases as the cube of the semimajor axis, and decreases as the reciprocal of the sum of the masses of the orbiting bodies increases.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 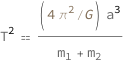 |
Use some values:
| Out[3]= | 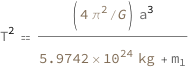 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["T", "Period"]^2 == (Quantity[4*Pi^2, "GravitationalConstant"^(-1)]*QuantityVariable["a", "Length"]^3)/(QuantityVariable[Subscript["m", "1"], "Mass"] + QuantityVariable[Subscript["m", "2"], "Mass"])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/191/191cdf30-b18a-4411-a83e-075038a13e35/Webpage/FormulaImage.png)