Value at Risk
Value at risk represents the amount of money at risk with a probability of p over a time period t.
The cutoff percentile approaches 1/2 as volatility increases. As the daily value at risk, or mean annual return, increases, the cutoff percentile decreases.
Formula
![Copy to Clipboard Erfc[(5*Sqrt[5]*(Log[Quantity[1, "USDollars"^(-1)]*QuantityVariable[Subscript["V", "i"], "Money"]] - Log[Quantity[-1, "USDollars"^(-1)]*QuantityVariable["VaR", "Money"] + Quantity[1, "USDollars"^(-1)]*QuantityVariable[Subscript["V", "i"], "Money"]] + QuantityVariable[Subscript["r", "m"], "Unitless"]/250))/QuantityVariable["σ", "Unitless"]]/2 == QuantityVariable["p", "Unitless"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/173/1734f0b4-3841-4ab1-b119-694dafc076bd/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| σ | volatility | "Unitless" |
| Vi | initial value | "Money" |
| VaR | daily value at risk | "Money" |
| rm | mean annual return | "Unitless" |
| p | cutoff percentile | "Unitless" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 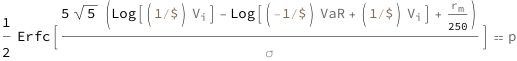 |
Use some values:
| In[3]:= |
| Out[3]= | 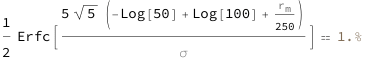 |