Relativistic de Broglie Angular Frequency by Momentum
The de Broglie angular frequency is the angular frequency associated with a massive particle in motion according to quantum mechanics, accounting for relativistic effects.
The de Broglie angular frequency is proportional to the mass plus the square root of the sum of the squares of the mass and the momentum.
Formula
![Copy to Clipboard QuantityVariable["ω", "AngularFrequency"] == Quantity[1, "ReducedPlanckConstant"^(-1)]*(Quantity[-1, "SpeedOfLight"^2]*QuantityVariable["m", "Mass"] + Sqrt[Quantity[1, "SpeedOfLight"^4]*QuantityVariable["m", "Mass"]^2 + Quantity[1, "SpeedOfLight"^2]*QuantityVariable["p", "Momentum"]^2])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/170/17061a30-d192-4e7e-b28b-5a81d9f512b1/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| ω | angular frequency | "AngularFrequency" |
| m | mass | "Mass" |
| p | momentum | "Momentum" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 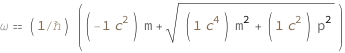 |
Use some values:
| In[3]:= | ![FormulaData[
ResourceObject[
"Relativistic de Broglie Angular Frequency by Momentum"], \
{QuantityVariable["\[Omega]","AngularFrequency"] ->
Quantity[1.`, ("Radians")/("Seconds")]}]](images/170/17061a30-d192-4e7e-b28b-5a81d9f512b1-io-3-i.en.gif) |
| Out[3]= | 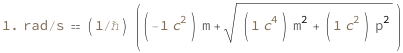 |