Cohen's d
Cohen's d is defined as the difference between two means divided by a standard deviation for the data.
Cohen's d depends directly on the difference between two sample means. Sample deviation and size are used to calculation a pooled standard deviation. As this measure increases, Cohen's d decreases inversely.
Formula
![Copy to Clipboard QuantityVariable["d", "Unitless"] == (QuantityVariable[Subscript[OverBar["x"], "1"], "Unitless"] - QuantityVariable[Subscript[OverBar["x"], "2"], "Unitless"])/Sqrt[((-1 + QuantityVariable[Subscript["n", "1"], "Unitless"])*QuantityVariable[Subscript["s", "1"], "Unitless"]^2 + (-1 + QuantityVariable[Subscript["n", "2"], "Unitless"])*QuantityVariable[Subscript["s", "2"], "Unitless"]^2)/(-2 + QuantityVariable[Subscript["n", "1"], "Unitless"] + QuantityVariable[Subscript["n", "2"], "Unitless"])]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/166/166064dc-931d-4f9c-842c-99191ad91af9/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| d | Cohen's d | "Unitless" |
| n1 | first sample size | "Unitless" |
| n2 | second sample size | "Unitless" |
| s1 | first sample standard deviation | "Unitless" |
| s2 | second sample standard deviation | "Unitless" |
| x̅1 | first sample mean | "Unitless" |
| x̅2 | second sample mean | "Unitless" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 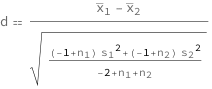 |
Use some values:
| In[3]:= |
| Out[3]= | 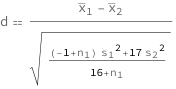 |