Equations of Motion for a Round Object on an Inclined Plane Using Slope
The equations of motion for a round object on an inclined plane are the equations that describe the behavior of the object in terms of its motion as a function of time. An inclined plane is a flat supporting surface tilted at an angle, with one end higher than the other.
The acceleration down an inclined plane equals the mass times the square of the radius of the object multiplied by the acceleration of gravity in the direction of the surface of the inclined plane divided by the sum of the moment of inertia and the mass times the square of the radius of the object.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 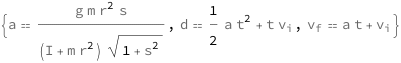 |
Use some values:
| Out[3]= |  |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable["a", "Acceleration"] == (QuantityVariable["g", "GravitationalAcceleration"]*QuantityVariable["m", "Mass"]*QuantityVariable["r", "Radius"]^2*QuantityVariable["s", "Unitless"])/((QuantityVariable["I", "MomentOfInertia"] + QuantityVariable["m", "Mass"]*QuantityVariable["r", "Radius"]^2)*Sqrt[1 + QuantityVariable["s", "Unitless"]^2]), QuantityVariable["d", "Distance"] == (QuantityVariable["a", "Acceleration"]*QuantityVariable["t", "Time"]^2)/2 + QuantityVariable["t", "Time"]*QuantityVariable[Subscript["v", "i"], "Speed"], QuantityVariable[Subscript["v", "f"], "Speed"] == QuantityVariable["a", "Acceleration"]*QuantityVariable["t", "Time"] + QuantityVariable[Subscript["v", "i"], "Speed"]}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/162/16280ce4-1d06-4137-b946-13c802b81c61/Webpage/FormulaImage.png)

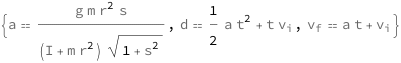
![FormulaData[
ResourceObject[
"Equations of Motion for a Round Object on an Inclined Plane Using \
Slope"], {QuantityVariable[
\!\(\*SubscriptBox[\("v"\), \("i"\)]\),"Speed"] ->
Quantity[0, ("Meters")/("Seconds")],
QuantityVariable["r","Radius"] -> Quantity[10, "Centimeters"],
QuantityVariable["s","Unitless"] -> 0.44`,
QuantityVariable["m","Mass"] -> Quantity[1, "Kilograms"],
QuantityVariable["t","Time"] -> Quantity[5, "Seconds"],
QuantityVariable["a","Acceleration"] ->
Quantity[1, ("Meters")/("Seconds")^2],
QuantityVariable["I","MomentOfInertia"] ->
Quantity[10, "Grams" ("Meters")^2]}]](images/162/16280ce4-1d06-4137-b946-13c802b81c61-io-3-i.en.gif)
