Gravitational Acceleration for a Uniform Density Sphere
Gravitational acceleration for a uniform density sphere is the acceleration on an object caused by the force of gravitation.
If the altitude of the object is greater than the sphere's radius, the gravitational acceleration is the product of the gravitational constant and the mass of the sphere divided by the sum of the sphere's radius and the altitude squared. If the altidue is less than the sphere's radius, then the gravitational acceleration is the product of the gravitational constant, the sum of the sphere's radius and the altitude, and the mass of the sphere divided by the sphere's radius cubed.
Formula
![Copy to Clipboard QuantityVariable["g", "GravitationalAcceleration"] == Piecewise[{{(Quantity[1, "GravitationalConstant"]*QuantityVariable["M", "Mass"])/(QuantityVariable["h", "Height"] + QuantityVariable["r", "Radius"])^2, QuantityVariable["h", "Height"] >= 0}, {(Quantity[1, "GravitationalConstant"]*QuantityVariable["M", "Mass"]*(QuantityVariable["h", "Height"] + QuantityVariable["r", "Radius"]))/QuantityVariable["r", "Radius"]^3, Inequality[-QuantityVariable["r", "Radius"], LessEqual, QuantityVariable["h", "Height"], Less, 0]}}, 0]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/160/16014ddb-d426-434a-a67e-75e5f7bcb0b0/Webpage/FormulaImage.png)
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 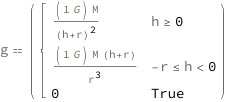 |
Use some values:
| In[3]:= | ![FormulaData[
ResourceObject[
"Gravitational Acceleration for a Uniform Density Sphere"], \
{QuantityVariable["h","Height"] -> Quantity[2, "Kilometers"],
QuantityVariable["M","Mass"] -> None,
QuantityVariable["g","GravitationalAcceleration"] ->
Quantity[9.80665`, ("Meters")/("Seconds")^2]}]](images/160/16014ddb-d426-434a-a67e-75e5f7bcb0b0-io-3-i.en.gif) |
| Out[3]= | 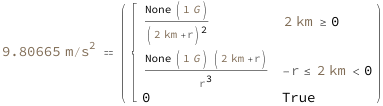 |