Moment of Inertia of an Ellipsoid
The mass moment of inertia measures the extent to which an object resists rotational acceleration about a particular axis, and is the rotational analog to mass. For a uniform solid ellipsoid, the moments of inertia are taken to be about the vertical axis passing through the ellipsoid's center of mass.
The moment of inertia of a uniform solid ellipsoid is proportional to the sum of the squares of the semiaxes of the ellipsoid and the mass.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 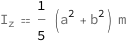 |
Use some values:
| Out[3]= | 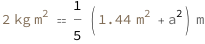 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable[Subscript["I", "z"], "MomentOfInertia"] == ((QuantityVariable["a", "Length"]^2 + QuantityVariable["b", "Length"]^2)*QuantityVariable["m", "Mass"])/5](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/150/1505a947-d86f-4e9c-90a5-1fa62201f0da/Webpage/FormulaImage.png)
