Ideal Rocket Equation
The ideal rocket equation describes the motion of vehicles that follow the basic principle of a rocket: a device that can apply acceleration to itself using thrust by expelling part of its mass with high velocity, and can thereby move due to the conservation of momentum.
The final speed equals the initial speed plus the effective exhaust velocity times the natural logarithm of the ratio of the initial mass of the rocket to the final mass.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 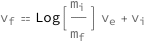 |
Use some values:
| Out[3]= | 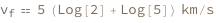 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable[Subscript["v", "f"], "Speed"] == Log[QuantityVariable[Subscript["m", "i"], "Mass"]/QuantityVariable[Subscript["m", "f"], "Mass"]]*QuantityVariable[Subscript["v", "e"], "Speed"] + QuantityVariable[Subscript["v", "i"], "Speed"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/148/1482a1fe-337f-47a1-83d2-e430447ef9c8/Webpage/FormulaImage.png)
