De Broglie Angular Frequency by Momentum

The de Broglie angular frequency is the angular frequency associated with a massive particle in motion according to quantum mechanics.

The de Broglie angular frequency equals half the square of the particle momentum divided by the reduced Planck constant and mass.

Formula

QuantityVariable["ω", "AngularFrequency"] == (Quantity[1/2, "ReducedPlanckConstant"^(-1)]*QuantityVariable["p", "Momentum"]^2)/QuantityVariable["m", "Mass"]

symbol	description	physical quantity
ω	angular frequency	"AngularFrequency"
m	mass	"Mass"
p	momentum	"Momentum"

Forms

Examples

Open in Wolfram Cloud

Download Example Notebook

Get the resource:

In[1]:=

Out[1]=

Get the formula:

In[2]:=

Out[2]=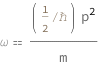

Use some values:

In[3]:=

$FormulaData[ ResourceObject[ "De Broglie Angular Frequency by Momentum"], {QuantityVariable[ "p","Momentum"] -> Quantity[1.67`*^-27, ("Kilograms" "Meters")/("Seconds")], QuantityVariable["\[Omega]","AngularFrequency"] -> Quantity[1, ("Radians")/("Seconds")]}]$

Out[3]=

Wolfram Formula Repository (Under Development)

De Broglie Angular Frequency by Momentum

Formula

Forms

Examples

External Links

Source Metadata

Publisher Information