Péclet Number Using Thermal Diffusivity
The Péclet number is a class of dimensionless numbers relevant in the study of transport phenomena in a continuum. It is defined to be the ratio of the rate of advection of a physical quantity by the flow to the rate of diffusion of the same quantity driven by an appropriate gradient.
The Pe'clet number for heat transfer equals the product of the characteristic length and characteristic speed divided by the thermal diffusivity.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 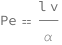 |
Use some values:
| Out[3]= |  |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["Pe", "PecletNumberHeatTransfer"] == (QuantityVariable["l", "Length"]*QuantityVariable["v", "Speed"])/QuantityVariable["α", "ThermalDiffusivity"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/10d/10d9ebbf-2b90-49f4-a713-cdcd496442d4/Webpage/FormulaImage.png)

![FormulaData[
ResourceObject[
"Péclet Number Using Thermal Diffusivity"], {QuantityVariable[
"v","Speed"] -> Quantity[1, ("Meters")/("Seconds")],
QuantityVariable["Pe","PecletNumberHeatTransfer"] -> 1,
QuantityVariable["\[Alpha]","ThermalDiffusivity"] ->
Quantity[1, ("Meters")^2/("Seconds")]}]](images/10d/10d9ebbf-2b90-49f4-a713-cdcd496442d4-io-3-i.en.gif)