Wolfram Computation Meets Knowledge

Wolfram Formula Repository (Under Development)

Spring Constant for Helical Spring

The spring constant is the stiffness of a spring—the force needed to stretch it a certian distance.

The spring constant increases linearly with spring wire diameter and its Young's modulus. It decreases with the Poisson ratio, the number of active windings and the cube of the spring's outer diameter.

Formula

QuantityVariable["k", "SpringConstant"] == (QuantityVariable["d", "Diameter"]^4*QuantityVariable["E", "YoungsModulus"])/(16*(-QuantityVariable["d", "Diameter"] + QuantityVariable["D", "Diameter"])^3*QuantityVariable["n", "Unitless"]*(1 + QuantityVariable["ν", "PoissonRatio"]))

symbol description physical quantity
k spring constant "SpringConstant"
d spring wire diameter "Diameter"
D spring outer diameter "Diameter"
E Young's modulus "YoungsModulus"
n number of active windings "Unitless"
ν Poisson ratio "PoissonRatio"

Forms

Examples

Get the resource:

In[1]:=
ResourceObject["Spring Constant for Helical Spring"]
Out[1]=

Get the formula:

In[2]:=
FormulaData[ResourceObject["Spring Constant for Helical Spring"]]
Out[2]=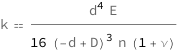

Use some values:

In[3]:=
FormulaData[ ResourceObject[ "Spring Constant for Helical Spring"], {QuantityVariable[ "\[Nu]","PoissonRatio"] -> 0.3`, QuantityVariable["d","Diameter"] -> Quantity[0.002`, "Meters"], QuantityVariable["n","Unitless"] -> 5, QuantityVariable["D","Diameter"] -> Quantity[0.01`, "Meters"]}]
Out[3]=

Publisher Information