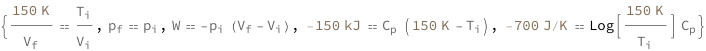Isobaric Process
An isobaric process is a thermodynamic process in which the pressure stays constant.
The final temperature divided by the final volume equals the initial temperature divided by the initial volume. The initial and final pressures are equal. The work done on the system equals the initial pressure times the difference between the initial and final volumes. The heat transferred to the system equals the isobaric heat capacity times the difference between the final and initial temperatures. The entropy change equals the isobaric heat capacity times the natural logarithm of the ratio of the final temperature to the initial temperature.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 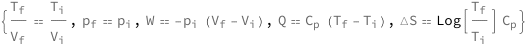 |
Use some values:
| Out[3]= | 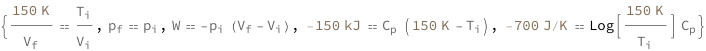 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable[Subscript["T", "f"], "Temperature"]/QuantityVariable[Subscript["V", "f"], "Volume"] == QuantityVariable[Subscript["T", "i"], "Temperature"]/QuantityVariable[Subscript["V", "i"], "Volume"], QuantityVariable[Subscript["p", "f"], "Pressure"] == QuantityVariable[Subscript["p", "i"], "Pressure"], QuantityVariable["W", "Work"] == -(QuantityVariable[Subscript["p", "i"], "Pressure"]*(QuantityVariable[Subscript["V", "f"], "Volume"] - QuantityVariable[Subscript["V", "i"], "Volume"])), QuantityVariable["Q", "Heat"] == QuantityVariable[Subscript["C", "p"], "HeatCapacity"]*(QuantityVariable[Subscript["T", "f"], "Temperature"] - QuantityVariable[Subscript["T", "i"], "Temperature"]), QuantityVariable["ΔS", "Entropy"] == Log[QuantityVariable[Subscript["T", "f"], "Temperature"]/QuantityVariable[Subscript["T", "i"], "Temperature"]]*QuantityVariable[Subscript["C", "p"], "HeatCapacity"]}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/0d9/0d9f3367-9ce1-452d-b3f2-8db0150f1fef/Webpage/FormulaImage.png)