Wolfram Computation Meets Knowledge

Wolfram Formula Repository (Under Development)

Gravitational Time Dilation Using Mass

Gravitational time dilation is a form of time dilation, an actual difference of elapsed time between two events as measured by observers situated at varying distances from a gravitating mass. The higher the gravitational potential (the farther the clock is from the source of gravitation), the faster time passes.

The time seen by a stationary observer equals the time in the rest frame divided by the square root of 1 minus twice the ratio of the gravitational constant times the mass of the gravitating object to the speed of light squared times the radius from the center of the massive object.

Formula

QuantityVariable["t", "Time"] == QuantityVariable[Subscript["t", "0"], "Time"]/Sqrt[1 + (Quantity[-2, "GravitationalConstant"/"SpeedOfLight"^2]*QuantityVariable["M", "Mass"])/QuantityVariable["r", "Radius"]]

Forms

Examples

Get the resource:

In[1]:=
ResourceObject["Gravitational Time Dilation Using Mass"]
Out[1]=

Get the formula:

In[2]:=
FormulaData[ResourceObject["Gravitational Time Dilation Using Mass"]]
Out[2]=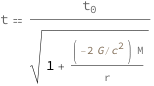

Use some values:

In[3]:=
FormulaData[ ResourceObject[ "Gravitational Time Dilation Using Mass"], {QuantityVariable[ "M","Mass"] -> Quantity[1, "SolarMass"], QuantityVariable[ \!\(\*SubscriptBox[\("t"\), \("0"\)]\),"Time"] -> Quantity[1, "Seconds"], QuantityVariable["r","Radius"] -> Quantity[12, "Kilometers"]}]
Out[3]=

Source Metadata

  • Creator:
  • Date: 1907

Publisher Information