Moment of Inertia of a Cone
The mass moment of inertia measures the extent to which an object resists rotational acceleration about a particular axis, and is the rotational analog to mass. For a uniform solid cone, the moments of inertia are taken to be about axes passing through the cone's center of mass.
The parallel moment of inertia increases with the square of the cone radius and the mass of the cone. The perpendicular moment of inertia increases with mass and the sum of the squares of the height of the cone and its radius.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 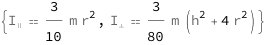 |
Use some values:
| Out[3]= | 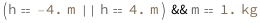 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable[Subscript["I", "∥"], "MomentOfInertia"] == (3*QuantityVariable["m", "Mass"]*QuantityVariable["r", "Radius"]^2)/10, QuantityVariable[Subscript["I", "⊥"], "MomentOfInertia"] == (3*QuantityVariable["m", "Mass"]*(QuantityVariable["h", "Height"]^2 + 4*QuantityVariable["r", "Radius"]^2))/80}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/098/098336cc-7c87-404e-bf6f-f0dff9f0c084/Webpage/FormulaImage.png)

![FormulaData[
ResourceObject[
"Moment of Inertia of a Cone"], {QuantityVariable["r","Radius"] ->
Quantity[1, "Meters"], QuantityVariable[
\!\(\*SubscriptBox[\("I"\), \("\[UpTee]"\)]\),"MomentOfInertia"] ->
Quantity[0.75`, "Kilograms" ("Meters")^2], QuantityVariable[
\!\(\*SubscriptBox[\("I"\), \("\[DoubleVerticalBar]"\)]\),
"MomentOfInertia"] ->
Quantity[0.30000000000000004`, "Kilograms" ("Meters")^2]}]](images/098/098336cc-7c87-404e-bf6f-f0dff9f0c084-io-3-i.en.gif)