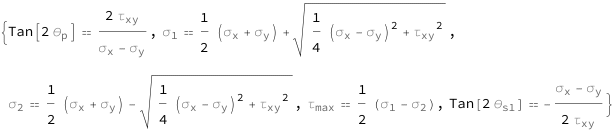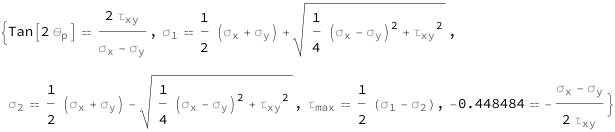Principal Stresses
At every point in a stressed body, there are at least three planes, called principal planes, with normal vectors, called principal directions, where the corresponding stress vector is perpendicular to the plane, i.e. parallel or in the same direction as the normal vector, and where there are no normal shear stresses. The three stresses normal to these principal planes are called principal stresses.
The tangent of twice the principal angle equals twice the shear stress divided by the difference between the normal stresses in the x and y directions. The maximum normal stress equals the average of the normal stresses in the x and y directions plus the square root of the sum of the shear stress squared and one-quarter of the square of the difference between the normal stresses in the x and y directions. The minimal normal stress equals the average of the normal stresses in the x and y directions minus the square root of the sum of the shear stress squared and one-quarter of the square of the difference between the normal stresses in the x and y directions. The maximum shear stress equals half the difference between the maximum and minimum normal stresses. The tangent of twice the maximum shear angle equals the difference between the normal stresses in the x and y directions divided by twice the shear stress.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 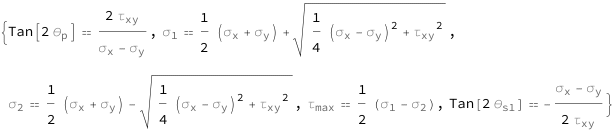 |
Use some values:
| Out[3]= | 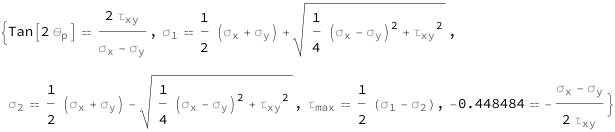 |
External Links
Publisher Information
![Copy to Clipboard {Tan[2*QuantityVariable[Subscript["θ", "p"], "Angle"]] == (2*QuantityVariable[Subscript["τ", "xy"], "Stress"])/(QuantityVariable[Subscript["σ", "x"], "Stress"] - QuantityVariable[Subscript["σ", "y"], "Stress"]), QuantityVariable[Subscript["σ", "1"], "Stress"] == (QuantityVariable[Subscript["σ", "x"], "Stress"] + QuantityVariable[Subscript["σ", "y"], "Stress"])/2 + Sqrt[(QuantityVariable[Subscript["σ", "x"], "Stress"] - QuantityVariable[Subscript["σ", "y"], "Stress"])^2/4 + QuantityVariable[Subscript["τ", "xy"], "Stress"]^2], QuantityVariable[Subscript["σ", "2"], "Stress"] == (QuantityVariable[Subscript["σ", "x"], "Stress"] + QuantityVariable[Subscript["σ", "y"], "Stress"])/2 - Sqrt[(QuantityVariable[Subscript["σ", "x"], "Stress"] - QuantityVariable[Subscript["σ", "y"], "Stress"])^2/4 + QuantityVariable[Subscript["τ", "xy"], "Stress"]^2], QuantityVariable[Subscript["τ", "max"], "Stress"] == (QuantityVariable[Subscript["σ", "1"], "Stress"] - QuantityVariable[Subscript["σ", "2"], "Stress"])/2, Tan[2*QuantityVariable[Subscript["θ", "s1"], "Angle"]] == -(QuantityVariable[Subscript["σ", "x"], "Stress"] - QuantityVariable[Subscript["σ", "y"], "Stress"])/(2*QuantityVariable[Subscript["τ", "xy"], "Stress"])}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/088/08885ecc-a578-4f30-b79d-9bcae1f0d389/Webpage/FormulaImage.png)