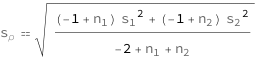Pooled Standard Deviation
Pooled standard deviation is the square root of the pooled variance. Pooled variance is a method for estimating the variance of several different populations when the mean of each population may be different, but one may assume that the variance of each population is the same.
The pooled standard deviation increases with the square root of the sum of the squares of the sample standard deviations weighted by the sample sizes.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 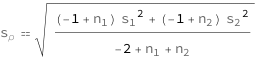 |
Use some values:
| Out[3]= | 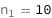 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable[Subscript["s", "ρ"], "Unitless"] == Sqrt[((-1 + QuantityVariable[Subscript["n", "1"], "Unitless"])*QuantityVariable[Subscript["s", "1"], "Unitless"]^2 + (-1 + QuantityVariable[Subscript["n", "2"], "Unitless"])*QuantityVariable[Subscript["s", "2"], "Unitless"]^2)/(-2 + QuantityVariable[Subscript["n", "1"], "Unitless"] + QuantityVariable[Subscript["n", "2"], "Unitless"])]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/06c/06c45561-cb5c-4ad6-8d39-58955dce2d69/Webpage/FormulaImage.png)