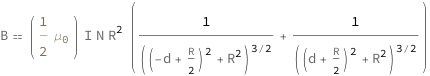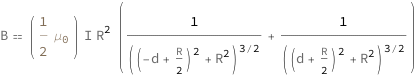Helmholtz Coil Field at Arbitrary Distance
A Helmholtz coil is a device for producing a region of nearly uniform magnetic field. It consists of two solenoid electromagnets on the same axis.
The magnetic flux density increases directly with the current and the number of coils. The magnetic flux density decreases with the radii of the coils. As the distance from the center of the Helmholtz coils increases, the field strength first increases (as it approaches the coil radius) and then declines.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 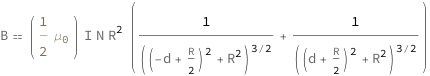 |
Use some values:
| Out[3]= | 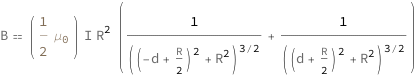 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["B", "MagneticFluxDensity"] == Quantity[1/2, "MagneticConstant"]*QuantityVariable["I", "ElectricCurrent"]*QuantityVariable["N", "Unitless"]*QuantityVariable["R", "Radius"]^2*(((-QuantityVariable["d", "Distance"] + QuantityVariable["R", "Radius"]/2)^2 + QuantityVariable["R", "Radius"]^2)^(-3/2) + ((QuantityVariable["d", "Distance"] + QuantityVariable["R", "Radius"]/2)^2 + QuantityVariable["R", "Radius"]^2)^(-3/2))](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/052/052625b3-ba02-42f5-8f6b-adc20ef8f9d8/Webpage/FormulaImage.png)