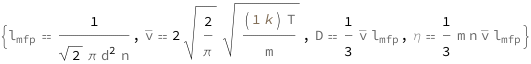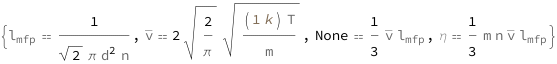Mean Free Path Using Electron Density
The mean free path is the average distance traveled by a moving particle (such as an atom, a molecule or a photon) between successive impacts (collisions), which modifies its direction, energy or other particle properties.
The mean free path is proportional to the reciprocal of the diameter squared times the particle number density. The mean speed is proportional to the square root of the temperature divided by the mass of the particle. The diffusion coefficient equals one-third of the mean speed times the mean free path. The dynamic viscosity equals one-third of the product of the mass of the particle, particle number density, mean speed and the mean free path.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 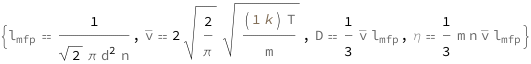 |
Use some values:
| Out[3]= | 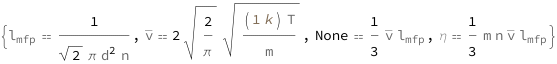 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable[Subscript["l", "mfp"], "MeanFreePath"] == 1/(Sqrt[2]*Pi*QuantityVariable["d", "Diameter"]^2*QuantityVariable["n", "InverseVolume"]), QuantityVariable[OverBar["v"], "Speed"] == 2*Sqrt[2/Pi]*Sqrt[(Quantity[1, "BoltzmannConstant"]*QuantityVariable["T", "Temperature"])/QuantityVariable["m", "Mass"]], QuantityVariable["D", "DiffusionCoefficient"] == (QuantityVariable[OverBar["v"], "Speed"]*QuantityVariable[Subscript["l", "mfp"], "MeanFreePath"])/3, QuantityVariable["η", "DynamicViscosity"] == (QuantityVariable["m", "Mass"]*QuantityVariable["n", "InverseVolume"]*QuantityVariable[OverBar["v"], "Speed"]*QuantityVariable[Subscript["l", "mfp"], "MeanFreePath"])/3}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/04c/04c805f9-2db8-4787-9780-d226f5377527/Webpage/FormulaImage.png)