Mohr's Circle Plane Shear Strain
Mohr's circle is a two-dimensional graphical representation of the transformation law for the Cauchy stress tensor. Strain is a description of deformation in terms of relative displacement of particles in the body that excludes rigid-body motions.
The shear strain in the new x\[Hyphen]y coordinates increases with the normal strain in the x and y directions (though a larger normal strain in the y direction will increase it more). Increased shear strain in the x\[Hyphen]y coordinates will also increase it.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 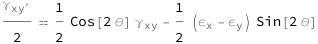 |
Use some values:
| Out[3]= | 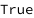 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable[Subscript["γ", Superscript["xy", "′"]], "Unitless"]/2 == (Cos[2*QuantityVariable["θ", "Angle"]]*QuantityVariable[Subscript["γ", "xy"], "Unitless"])/2 - ((QuantityVariable[Subscript["ε", "x"], "Unitless"] - QuantityVariable[Subscript["ε", "y"], "Unitless"])*Sin[2*QuantityVariable["θ", "Angle"]])/2](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/043/0438d425-9e35-45ba-8585-bb1492077e40/Webpage/FormulaImage.png)
