Kepler's First Law
Kepler's laws of planetary motion are three scientific laws describing the motion of planets around the Sun. The first law states that the orbit of a planet is an ellipse with the Sun at one of the two foci.
The orbital radius increases as the semimajor axis increases, and varies based on phase and eccentricity of the orbit.
Formula
![Copy to Clipboard QuantityVariable["r", "Radius"] == (QuantityVariable["a", "Length"]*(1 - QuantityVariable["e", "Unitless"]^2))/(1 + Cos[QuantityVariable["θ", "Angle"]]*QuantityVariable["e", "Unitless"])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/012/01200bb4-0d0e-447c-af03-46a74503811b/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| r | radius | "Radius" |
| a | semimajor axis | "Length" |
| θ | phase | "Angle" |
| e | eccentricity | "Unitless" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 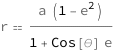 |
Use some values:
| In[3]:= | ![FormulaData[
ResourceObject[
"Kepler's First Law"], {QuantityVariable["r","Radius"] ->
Quantity[1.49597887`*^8, "Kilometers"],
QuantityVariable["a","Length"] ->
Quantity[1.49597887`*^8, "Kilometers"]}]](images/012/01200bb4-0d0e-447c-af03-46a74503811b-io-3-i.en.gif) |
| Out[3]= | 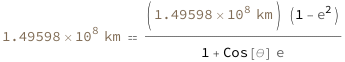 |