Glass's δ
Glass's δ is an estimator of the population effect size that uses only the standard deviation of the second group. An effect size is a quantitative measure of the strength of a phenomenon. A population effect size based on means considers the standardized mean difference between two populations.
Glass's \[Delta] equals the differences between the first and second sample means divided by the second sample standard deviation.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 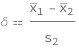 |
Use some values:
| Out[3]= | 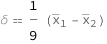 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["δ", "Unitless"] == (QuantityVariable[Subscript[OverBar["x"], "1"], "Unitless"] - QuantityVariable[Subscript[OverBar["x"], "2"], "Unitless"])/QuantityVariable[Subscript["s", "2"], "Unitless"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/009/00992b35-37dd-4984-8118-9f5b058e1ba1/Webpage/FormulaImage.png)
