Wolfram Language Paclet Repository
Community-contributed installable additions to the Wolfram Language
QuantumMeasurementOperator |
|
| | ||||
|
| | ||||
|
| | ||||
| | |||||
QuantumMeasurementOperator |
|
QuantumMeasurementOperator |
|
QuantumMeasurementOperator |
|
QuantumState |
 |
|
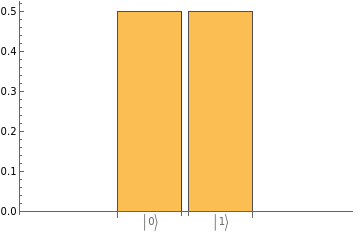
QuantumState |
|
QuantumMeasurementOperator |
QuantumBasis |
|

QuantumMeasurementOperator |
|
QuantumMeasurementOperator |
QuantumState |

QuantumMeasurementOperator |
|
QuantumState |
QuantumMeasurementOperator |