Wolfram Language Paclet Repository
Community-contributed installable additions to the Wolfram Language
Work with logical functions and boolean values
Contributed by: Peter Cullen Burbery
This paclet contains helpful functions for boolean logic. I give credit to the authors of FindBooleanAlternative, Stephen Wolfram and Nikolay Murzin. I want to compile helpful functions for logic into one place.

To install this paclet in your Wolfram Language environment,
evaluate this code:
PacletInstall["PeterBurbery/BooleanLogic"]
To load the code after installation, evaluate this code:
Needs["PeterBurbery`BooleanLogic`"]
Find an alternative form of p implies q and r with xor and nand:
| In[1]:= |
| Out[1]= |
Find seven other alternatives:
| In[2]:= |
| Out[2]= |
Make a Venn diagram for b, c, and d:
| In[3]:= |
| Out[3]= | 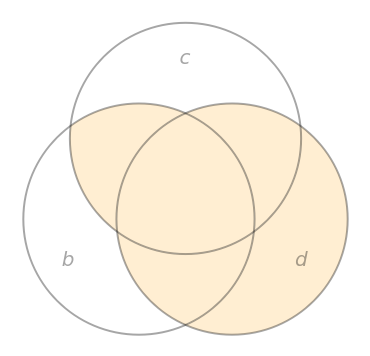 |
Add the input e to the Venn Diagram:
| In[4]:= |
| Out[4]= | 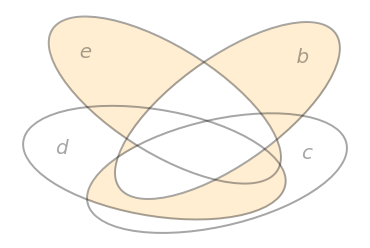 |
VennDiagram can accept up to 5 variables:
| In[5]:= |
| Out[5]= | 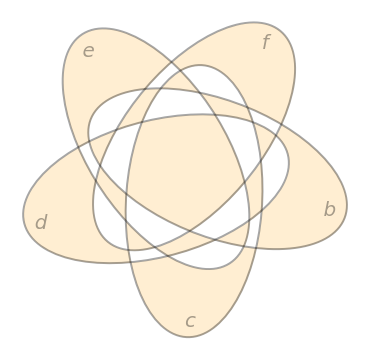 |
Make a Venn diagram using BooleanFunction as input:
| In[6]:= |
| Out[6]= | 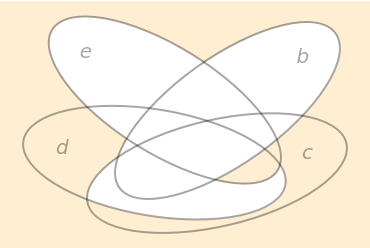 |
Create a Venn diagram by using sets as input:
| In[7]:= |
| Out[7]= | 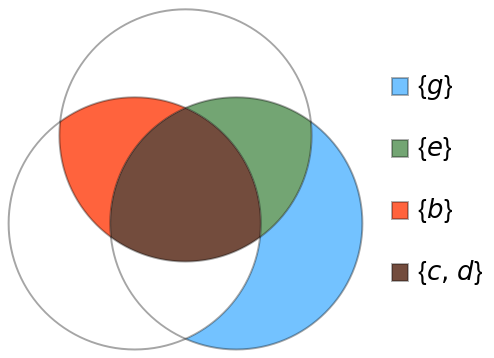 |
Create a Venn diagram by using Not and Or canonical normal form as input:
| In[8]:= |
| Out[8]= | 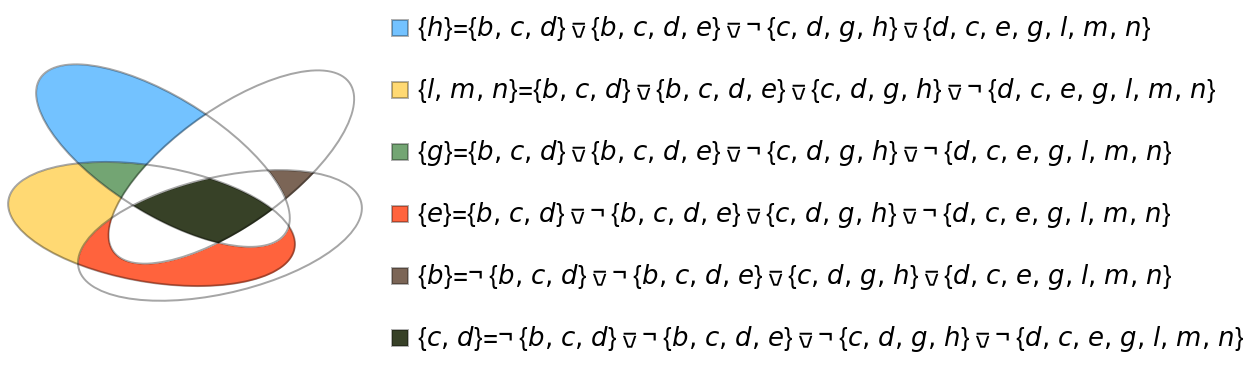 |
| In[9]:= |
| Out[9]= | 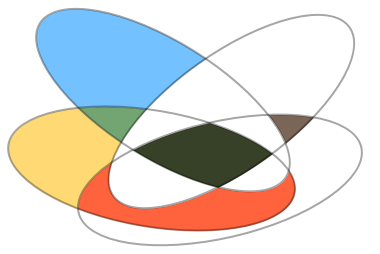 |
Find information on a boolean function's structure:
| In[10]:= |
| Out[10]= |  |
Find information on the output given true inputs and false inputs, including whether the problem is satisfiable. This is helpful when working on the NP-complete problem 3SAT:
| In[11]:= |
| Out[11]= |
Evaluate the NP complete 17SAT problem:
| In[12]:= |
| Out[12]= |  |
Generate a truth table for a function with 4 inputs:
| In[13]:= |
| Out[13]= | 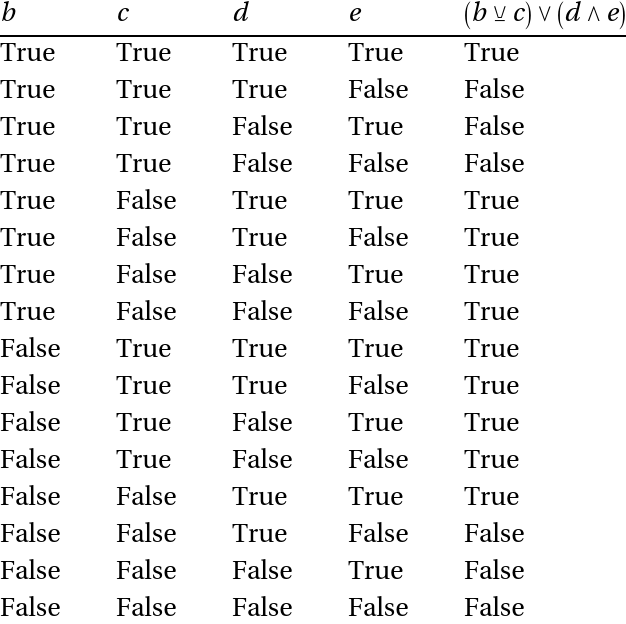 |
Use 1 and 0 in place of true and false, respectively:
| In[14]:= |
| Out[14]= |  |
Wolfram Language Version 13.1