Wolfram Language Paclet Repository
Community-contributed installable additions to the Wolfram Language
Automata theory package
Contributed by: sutner@cmu.edu
Automata supports computation with finite state machines, syntactic semigroups and one-dimensional cellular automata.
To install this paclet in your Wolfram Language environment,
evaluate this code:
PacletInstall["KlausSutner/Automata"]
To load the code after installation, evaluate this code:
Needs["KlausSutner`Automata`"]
Construct a finite state machine that accepts all words with an a in the third position from the end:
| In[1]:= |
| In[2]:= |
| Out[2]= |
Generate a few words in the language to verify correctness:
| In[3]:= |
| Out[3]= |
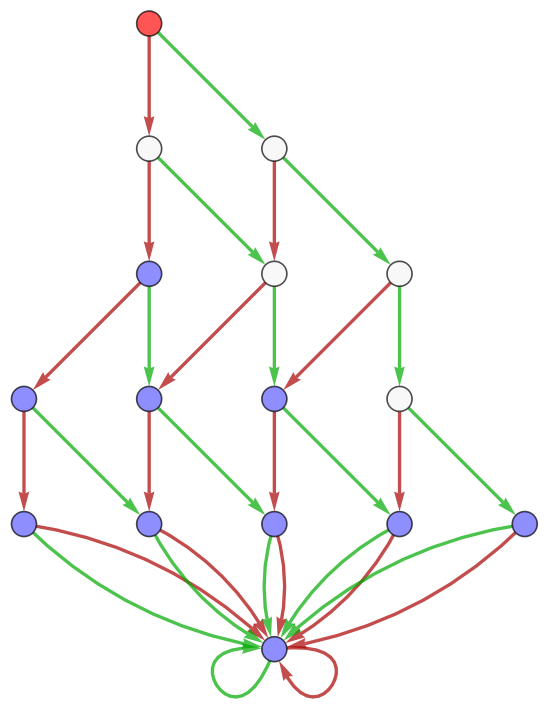
Plot the diagram of the machine, using edge labels or colors:
| In[4]:= |
| Out[4]= |  |
| In[5]:= |
| Out[5]= | 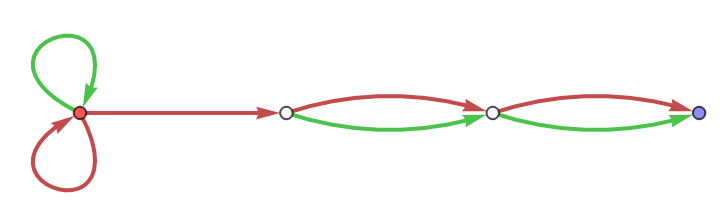 |
Determinize the machine to obtain a DFA. The machine exhibits exponential blowup during determinization:
| In[6]:= |
| Out[6]= |
We can check the growth function of the DFA as further evidence of correctness:
| In[7]:= |
| Out[7]= |
The DFA produced by determinization is already minimal:
| In[8]:= |
| Out[8]= |
We construct the syntactic semigroup of the language and test some of its properties:
| In[9]:= |
| Out[9]= |
| In[10]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/8e445fd5-6995-4418-848f-fdfada0e2d62"]](https://www.wolframcloud.com/obj/resourcesystem/images/6a5/6a5a71eb-13cb-4554-a920-7cb3ae87a8b8/10592679d686d3d3.png) |
| Out[10]= |  |
A one-dimensional cellular automaton has surjective global map iff the associated semiautomaton is universal. We use this method to determine all surjective elementary cellular automata:
| In[11]:= |
| Out[11]= |
A better quadratic time algorithm classifies cellular automata into injective/open/surjective/none:
| In[12]:= |
| Out[12]= |
Thus there are 6 injective ECA, 8 open ones, and so on.
Wolfram Language Version 13.1
Creative Commons Attribution Non Commercial No Derivatives 4.0 International