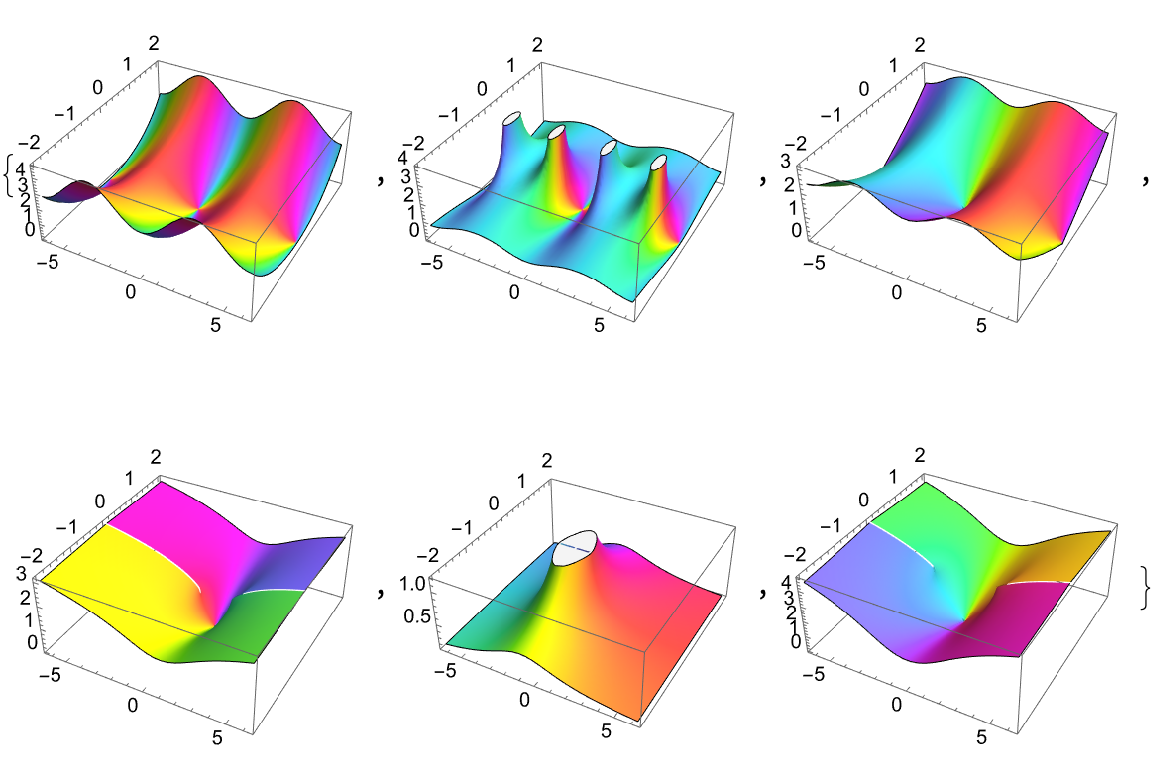
In a standard trigonometry course, we typically learn about six functions (and their inverses): sin(x), cos(x), tan(x), csc(x), sec(x), and tan(x); this may or may not be extended later to cover the six hyperbolic trig functions (e.g. sinh(x)) and/or their inverses (e.g. sin-1(x), sinh-1(x)).
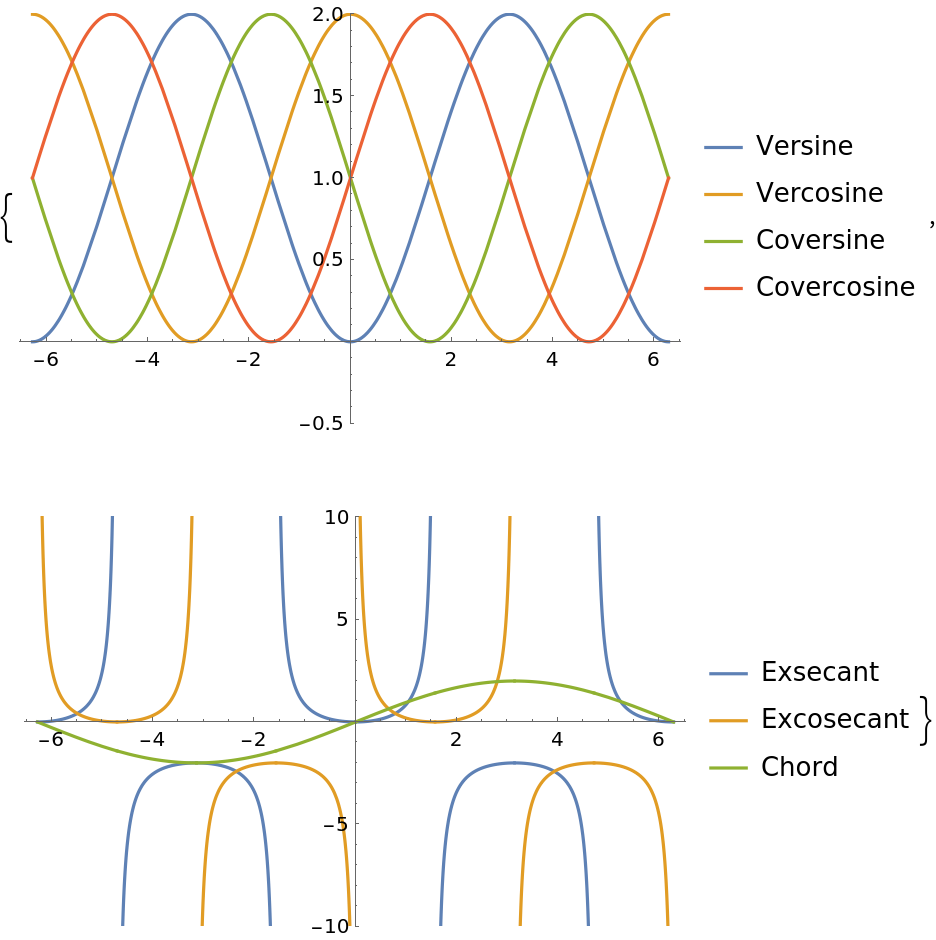
A less-known fact is that trigonometry actually consists of over two dozen other circular and hyperbolic functions, each of which has a well-defined inverse. These mysterious trig functions are closely related to the more well-known relatives that we all know and love today, and though they're rarely used, these functions were ubiquitous a few centuries back, being employed both in academia and in various applications (e.g. mapmaking, ocean exploration, etc.).
Mathematica has a couple of these little-used trig functions built in (namely Haversine and InverseHaversine), but the rest remain unrepresented; this absence is the underlying motivation for Trigonometry. All of the 50+ functions in Trigonometry work naturally with the entire Wolfram Language framework, and their immediate availability allows a better understanding of the relationships and history of both trigonometry and mathematics as a whole. These functions provide both a learning opportunity and a teaching tool, thus contributing to the enrichment of mathematics as a whole.

![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/fb894474-9b27-4573-839c-9b7eb5fa4c02"]](https://www.wolframcloud.com/obj/resourcesystem/images/d91/d914e9d4-2be0-4478-8342-578434d19777/1-2-0/5b4db9a1a1b6b63e.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/9a36d649-5050-4705-b2c6-a343e4abace8"]](https://www.wolframcloud.com/obj/resourcesystem/images/d91/d914e9d4-2be0-4478-8342-578434d19777/1-2-0/7b674b0e1635714c.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/840bf621-4ddb-4ad1-b031-50f6dee7173c"]](https://www.wolframcloud.com/obj/resourcesystem/images/d91/d914e9d4-2be0-4478-8342-578434d19777/1-2-0/52cee7615e4b9902.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/bed2c331-40d5-4b2a-b21e-7fc3d0c408e4"]](https://www.wolframcloud.com/obj/resourcesystem/images/d91/d914e9d4-2be0-4478-8342-578434d19777/1-2-0/28703cc78f570fa9.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/766e5bed-a694-4967-a98b-1473e41b12f0"]](https://www.wolframcloud.com/obj/resourcesystem/images/d91/d914e9d4-2be0-4478-8342-578434d19777/1-2-0/7f294cffe258a098.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/fc1ad750-9073-4014-928a-92486ff31f20"]](https://www.wolframcloud.com/obj/resourcesystem/images/d91/d914e9d4-2be0-4478-8342-578434d19777/1-2-0/0ab3d67aa0cb2363.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/c08ad3a9-ec80-4870-aedf-eb3fe94b1aa3"]](https://www.wolframcloud.com/obj/resourcesystem/images/d91/d914e9d4-2be0-4478-8342-578434d19777/1-2-0/3a88074f5ea6b64c.png)
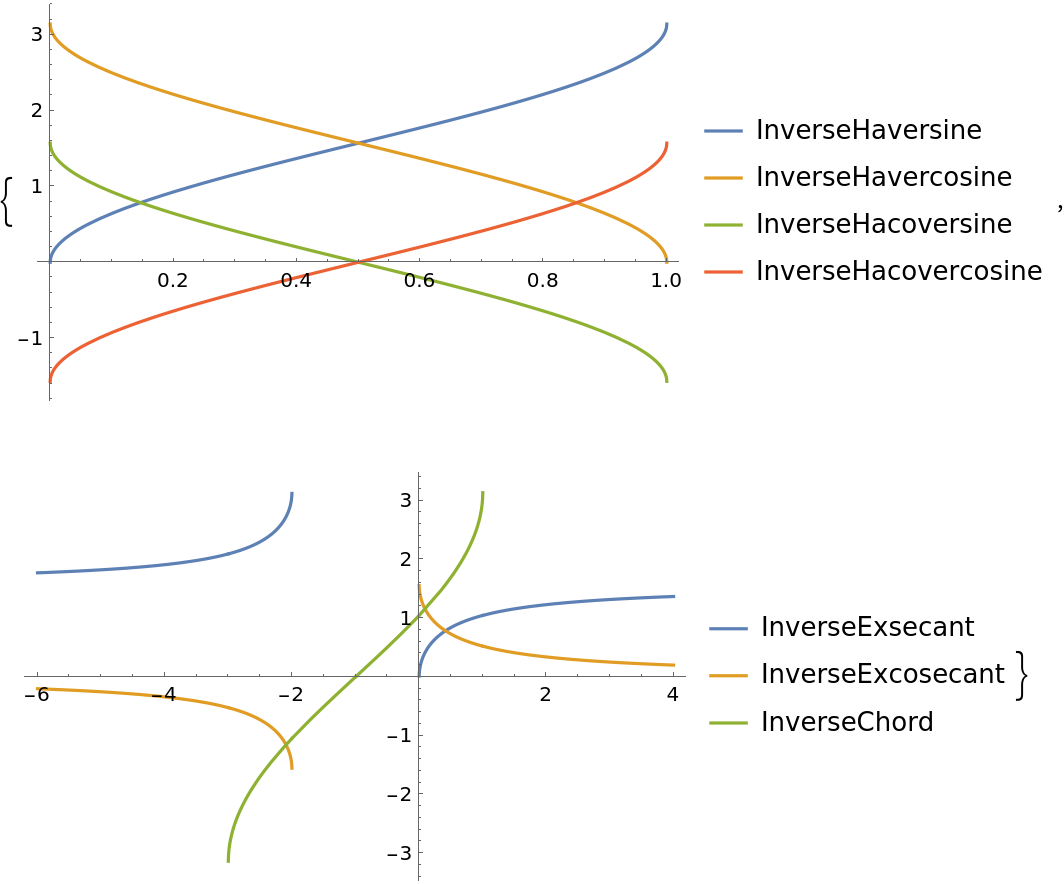
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/39f22ab1-fec9-473a-836b-5e517930d729"]](https://www.wolframcloud.com/obj/resourcesystem/images/d91/d914e9d4-2be0-4478-8342-578434d19777/1-2-0/00d14fa5419f6268.png)