DuganHammock/
ConvexPolytope
Installation Instructions
To install this paclet in your Wolfram Language environment,
evaluate this code:
PacletInstall["DuganHammock/ConvexPolytope"]
To load the code after installation, evaluate this code:
Needs["DuganHammock`ConvexPolytope`"]
Examples
Basic Examples
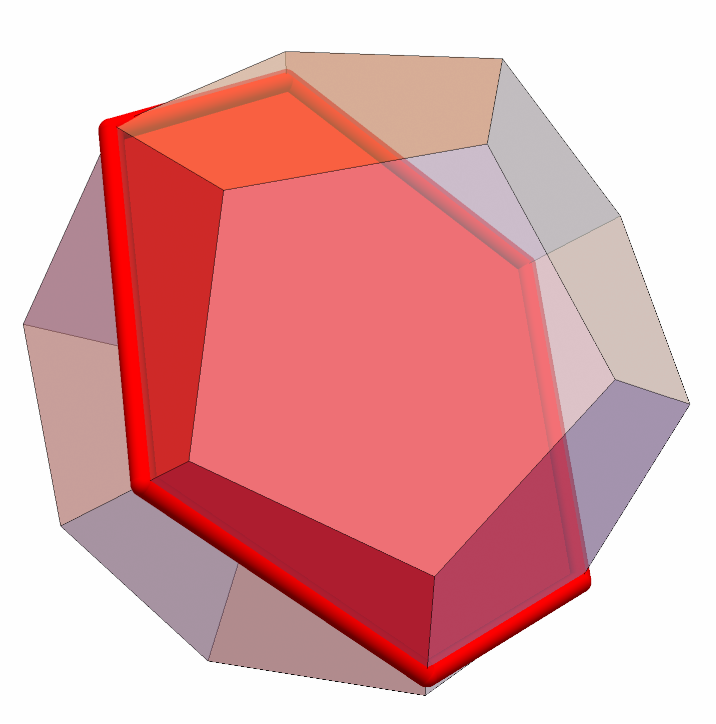
Hexagon as equatorial slice of a dodecahedron:
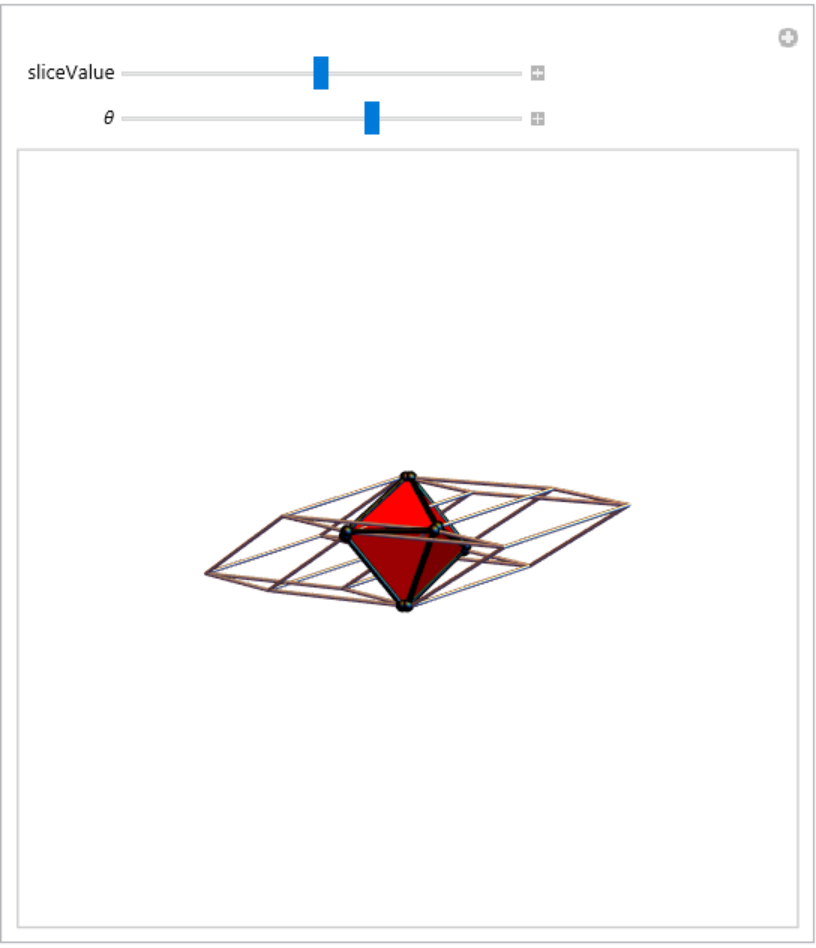
4D hypercube (tesseract):
600-cell (hexacosichoron):
120-cell (dodecacontachoron):
Publisher
Dugan Hammock
Compatibility
Wolfram Language Version 13.3
Version History
- 1.0.3
– 15 May 2025
- 1.0.2
– 26 July 2023
- 1.0.1
– 21 July 2023
- 1.0.0
– 19 July 2023
MIT License
Paclet Source

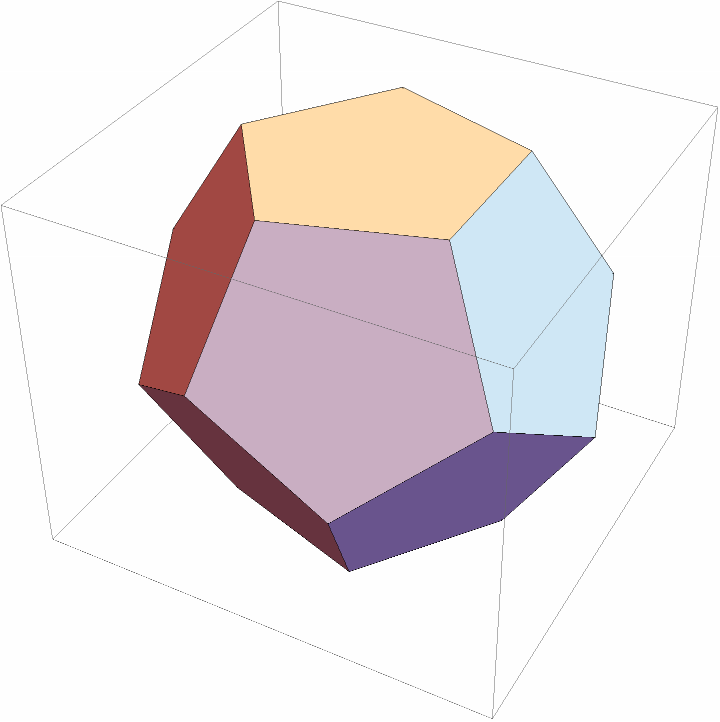
![polytope = PolyhedronData["Dodecahedron", "VertexCoordinates"] // N // ConvexPolytope;
polytope = Join[polytope["Vertices"], Map[Mean, polytope["Facets"]]] // Map[Normalize] // ConvexPolytope;
polytope // Polygon // Graphics3D](https://www.wolframcloud.com/obj/resourcesystem/images/703/703e94b5-7e08-4c0f-ac24-9023cf425fe2/71c9c417392b648e.png)
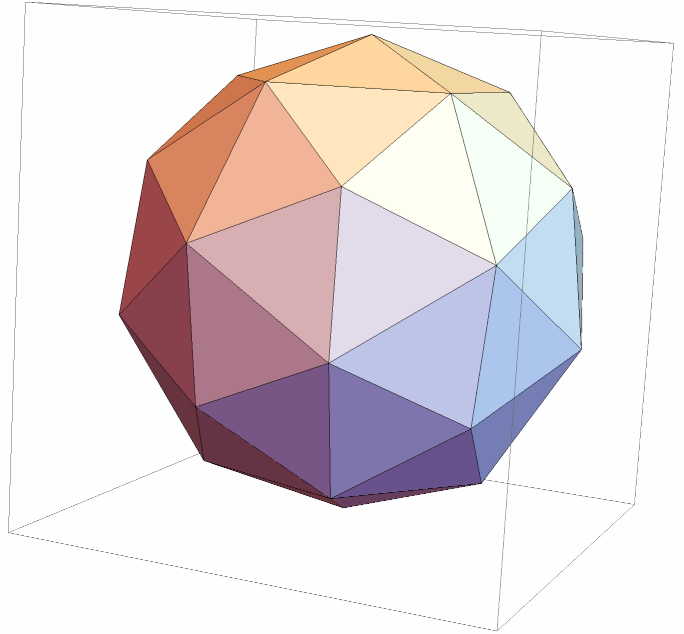
![polytope = PolyhedronData["Dodecahedron", "VertexCoordinates"] // N // ConvexPolytope;
polytope = Join[polytope["Vertices"], Map[Mean, polytope["Facets"]]] // Map[Normalize] // ConvexPolytope;
polytope = Join[polytope["Vertices"], Map[Mean, polytope["Facets"]]] // Map[Normalize] // ConvexPolytope;
polytope // Polygon // Graphics3D](https://www.wolframcloud.com/obj/resourcesystem/images/703/703e94b5-7e08-4c0f-ac24-9023cf425fe2/28a3b86c6539d1e9.png)
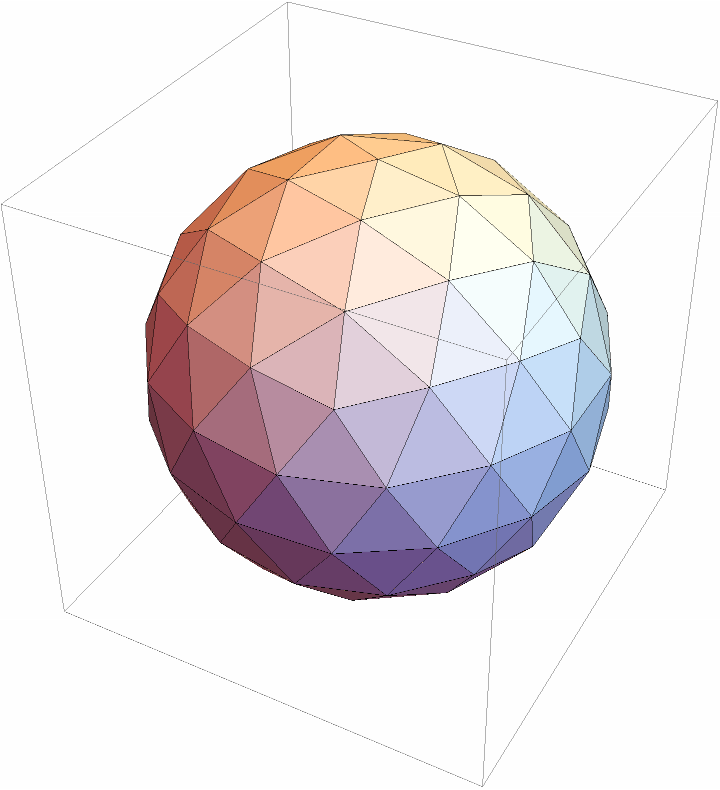
![polytope = PolyhedronData["Dodecahedron", "VertexCoordinates"] // N // ConvexPolytope;
polytope = Join[polytope["Vertices"], Map[Mean, polytope["Facets"]]] // Map[Normalize] // ConvexPolytope;
polytope = Join[polytope["Vertices"], Map[Mean, polytope["Faces", 1]]] // Map[Normalize] // ConvexPolytope;
polytope = polytope // ConvexPolytopeDual;
polytope // Polygon // Graphics3D // Print;](https://www.wolframcloud.com/obj/resourcesystem/images/703/703e94b5-7e08-4c0f-ac24-9023cf425fe2/659f870c67968f19.png)
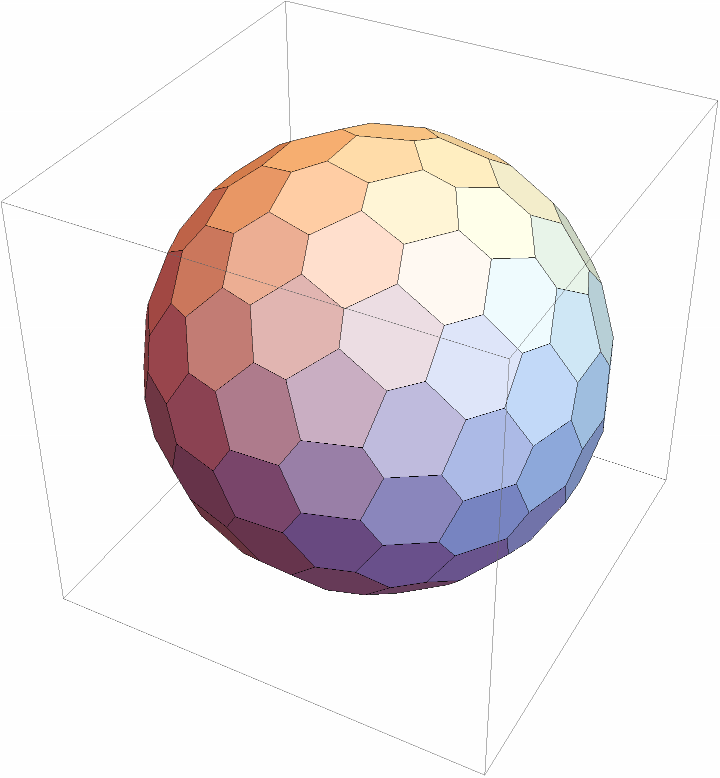
![polytope = PolyhedronData["Dodecahedron", "VertexCoordinates"] // N // ConvexPolytope;
polytopeSlice = polytope["Slice", {1, 1, 1}, 0.0];
Graphics3D[{
{Opacity[0.5], polytope // Polygon},
{Red, polytopeSlice // Polygon},
{Red, polytopeSlice // Tube[.05]},
}, Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/703/703e94b5-7e08-4c0f-ac24-9023cf425fe2/651ba92187cc2137.png)
![Manipulate[
skewMatrix4D = {{1, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, 1, 0}, {3, 1, 1, 1}};
hypercubeVertices = Tuples[{-1, 1}, {4}] // N // Map[Normalize];
hypercubeVertices = hypercubeVertices . RotationMatrix[\[Theta], {{1, 1, 1, 1}, {0, 0, 0, 1}}]\[Transpose];
hypercubeVertices = hypercubeVertices . skewMatrix4D;
hypercubePolytope = hypercubeVertices // N // ConvexPolytope;
hypercubeSlicePolytope = hypercubePolytope["Slice", {0, 0, 0, 1}, sliceValue];
Graphics3D[{
Specularity[1, 20],
{Gray, hypercubePolytope // Tube[.03]},
If[Positive[hypercubeSlicePolytope["Dimension"]],
{
{Red, hypercubeSlicePolytope // Polygon},
{Black, hypercubeSlicePolytope // Tube[0.05]},
{Black, hypercubeSlicePolytope // Sphere[0.1]}
}
]
}
, PlotRange -> 3
, Boxed -> False
]
, {{sliceValue, 0.}, -1, 1}
, {{\[Theta], 1}, 0., Pi/2.}
, {skewMatrix4D, None}
, {hypercubeVertices, None}
, {hypercubePolytope, None}
, {hypercubeSlicePolytope, None}
, TrackedSymbols :> {sliceValue, \[Theta]}
]](https://www.wolframcloud.com/obj/resourcesystem/images/703/703e94b5-7e08-4c0f-ac24-9023cf425fe2/677f217bcf5af716.png)
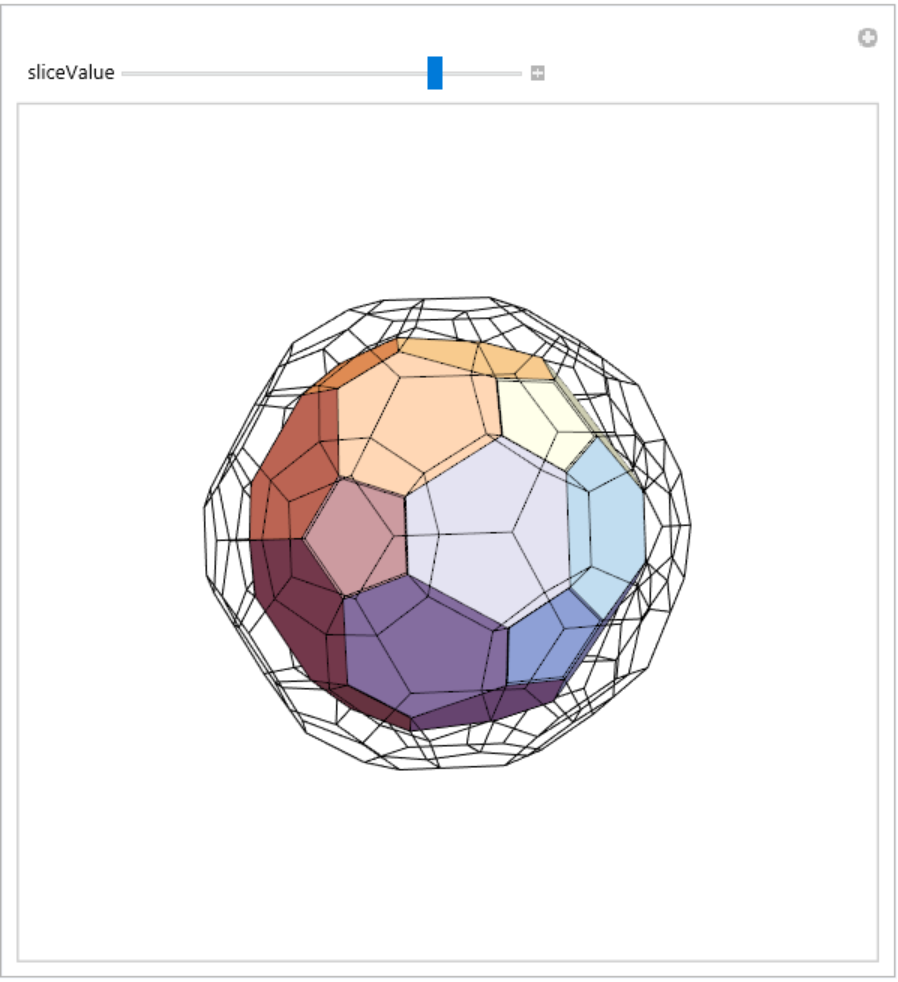
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/8a600eae-0126-42bf-98e9-a8316f1925f5"]](https://www.wolframcloud.com/obj/resourcesystem/images/703/703e94b5-7e08-4c0f-ac24-9023cf425fe2/56646e4e1e582e4c.png)
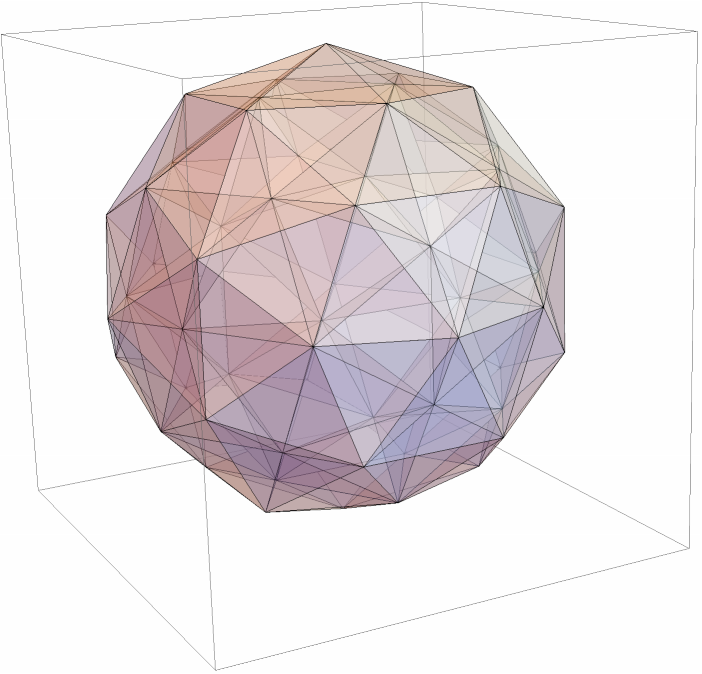
![c600Polytope = DuganHammock`ConvexPolytope`ConvexPolytope[<|"Dimension" -> 4, "EmbeddingDimension" -> 4, "VertexCoordinates" -> CompressedData["
1:eJydlr1NA0EQhVeIRqiAkHBaQJSAREwInRC4AbpwRgM0gETkCAcUAIFnT35z
n974VrKs27dvd/5nbh6fH56uxhiv/7/rkeu4H7Def992L9+HE/41z90fbu9+
Pj73Bo/E87yeAzzW31/ezXsMHoCH4YfylQfyTx7Yb+6D/RQvcp7rl6vgofjG
/7hwX/F5TuXWuAHc2dvFE/HD8EP5aleQX3G1U9du7tv5pZxb1ztXwU2cLjyD
Fzs387m8D/K6fCB9oS4VXOWneqI42a/kpcHlu1+nm/mGdcrwS5yAPi5eiF/s
DLirp65fGT8hv9T588V+uuzcke4v++t24358wku/MforXuK1Ww8o3o3/Fcd6
6/qJqdcU/4prfjb9MvVx8V76UHOegTliedfNC9QPUi7D1/oZygP5Ka/LPtgP
6me73qM++R78d/vx1j7frccYr8pz87aZZ0tfBBzzxfWTdfk329nd487BPJCL
4p3n2Ga/oTmk+Nn5Q9/NewyO+Wj4ZLeiJ8UL2M/1a5CD+ugYf0q1vXw=
"], "FaceVertexIndices" -> <|0 -> {{1}, {2}, {3}, {4}, {5}, {6}, {
7}, {8}, {9}, {10}, {11}, {12}, {13}, {14}, {15}, {16}, {17}, {
18}, {19}, {20}, {21}, {22}, {23}, {24}, {25}, {26}, {27}, {
28}, {29}, {30}, {31}, {32}, {33}, {34}, {35}, {36}, {37}, {
38}, {39}, {40}, {41}, {42}, {43}, {44}, {45}, {46}, {47}, {
48}, {49}, {50}, {51}, {52}, {53}, {54}, {55}, {56}, {57}, {
58}, {59}, {60}, {61}, {62}, {63}, {64}, {65}, {66}, {67}, {
68}, {69}, {70}, {71}, {72}, {73}, {74}, {75}, {76}, {77}, {
78}, {79}, {80}, {81}, {82}, {83}, {84}, {85}, {86}, {87}, {
88}, {89}, {90}, {91}, {92}, {93}, {94}, {95}, {96}, {97}, {
98}, {99}, {100}, {101}, {102}, {103}, {104}, {105}, {106}, {
107}, {108}, {109}, {110}, {111}, {112}, {113}, {114}, {115}, {
116}, {117}, {118}, {119}, {120}}, 1 -> CompressedData["
1:eJwVxVWigggAAMAndncnYnd3N7bYrdiJrcfcI+3uzwyIYggK/P39/fMf/48D
cHgcAUfEkXBkHAVHxdFwdBwDxwTwAAEgAiSAArAANsABeIAA0OIJeCKejKfi
WXg2novn44V4iEAikAk0AovAIXAJIoKYoCNSiFQincgm8oh8ooQoJepJFBKN
xCBxSAKSiCQjKUgGMpVMIzPJXLKQLCbLyUqykUKnMCg8ioAiocgoKoqJSqcy
qXyqkCqlyqlqqpnGoDFpIpqYpqApaRqahc6gM+kSupSuoqvpIN3KYDJkDAVD
xdAwQIaNKWcqmWqmhgky7Sw2i8PisrQsiKVjOVhOlovNY/PZWjbE1rMdbDfb
wxFwRBwtR8cxcJwcLyfIFXLFXIir4xq5Lq6PG+IJeBKelqfnmXhunp8X5gv5
Uj7E1/PNfA8/wI8IZAKtwCAwCbwCvyAmlAshoVFoFvqEAWFcJBYpRDqRQWQR
BUVRUVKsFOvERrFFHBJHxSmJVKKS6CUmiVUSliQkaalaqpeapVZpRJqQZmQK
mUpmkJlkNllMlpXl5Uq5Wm6Um+V2eVyekxcUGoVBYVHYFElFVlFUapRGpUVp
V6aUOWVJBapMKqvKpkqr8ipYDarNaqvars6oC+qyBtRYNDaNXVPUlDQV0Ara
QDsIg2WwonVonVq31qv1a6uQA3JBHsgHBaCazqlz6YK6kC6qq+vdeo8+rI/o
E/qGwWsIGmKGpCFraBp9xpAxbkwZc8aWyW8Km2KmtClvQswBc8QcN2fMBXPb
ErUkLSlL0VKydKwJa9qascLWsrVry9rytqINtlVsPXvOXrCX7GV7xd53OB0u
h9vhcVQdNcfAMXS6nF5n0Fl11p0D58jlc4VcNVfdNXCN3R633x12V90N99A9
8QQ8EU/N0/AMPVOv3xv0xrxVb9M78s58AV/IF/fVfC3f2Df3h/0xf9WP+Cf+
WSASiAdqgXZgGpgHo8FksB5sBkfBRSgaSoXqoVZoHFqGE+F0uBFGwpMwGklE
MpFGpB2ZRlbRZDQVrUc70UV0GcvG8rFmDInNYut4Ll6It+Lt+Dy+SaQTmUQj
0U2giVUymywmm8lOcpHcpnKpUqqV6qSWqV06n4bTSLqbRtP7TCFTzrQz3cwq
c8jms8VsM9vLrrPbXCFXyrVy/dwmt8vDeSTfy6/z+0K50C70C5vCoVgqVoqd
Yq+4LR5LlVKn1C/tSke4DFfgLtyD9/CpXCl3y/3yoXyq9Cr9yrFyqg6qw+qo
OqnOqufaoDasjWvT2rx2qQ/qo/q4vqgv69fGsDFpTBtoY9XAmqPmrLlorpvb
5q01bs1by9amtWvdkQkyQ1BkjeyRR3vanrdX7U370H52Fp1lZ9vZdY6dVxft
rrr77qF76r576962t+8de6fep7/p7/qH/rF/6n8Hw8FoMB6cB5fBdTgZTofn
4WWIjWajxeg8uo5u4/l4Ob6Mr+P7ZDZBJ+cJNnlM59PV9DLFps/Zenae3WaP
+WZ+md/nz8VysV1cF7fFa7lbXpf35QtdoXsUQx/oe3VYYavn6r3ervfr2/qx
/mx2m8Pmvnluvtvj9rZ9bT+74+6+e+2++9P+sX/vP4fT4Xl4H77H0/F1/By/
p/fpc/qeL+frGTvfzo/z73K9YJf75Xn5XW/X+/V1/WEP7Im9sd/tcXvdPrff
/Xl/3b/33+P9+Dx+z/fz+/y9Pq/v6/f+vL/v3+f7+X1//wI+yFbc
"], 2 -> CompressedData["
1:eJwNxePC8gwAANCnbdk2lm3b5rJrmct1We8lft/5c2AUQ1Dg7+/vH/T3B/4/
DgBxAIQD8DiAgANIOBDCgXgcSMSBZBxEwEFEHETB4Uk4PBmHp+IIJByBgiPQ
cEQyjkjBEek4EhVHouHIVByZjqPQcBQ6jkrDUek4Gh0AIQDEAyADAJkARAAg
BgCxADwJwDMBPAcgkAACCyDwABIHIPEABhNgsACGGmByAKYaYPEAlhrg8ACO
GuCpQYgIQgwQYoN4MohngnguSCSDRDZI5INkLkjmgwwmyGCDDA3I5IJMDcjm
g2wNyOWDXA3I10AECkRgQQQBRKRARDZEFEIUAUQRQgwWxGBDDC3EEkAsLcQW
QmwtJBBCAi0k1OJJVDyJgyeJ8GQqnszFk8V4qghPFeOZHDyTi2fq8BwRnqPD
c8V4rg4vEuNFOrxYRyDRCCQegSQhUGgEioBAkRFoEgJNRmDxCCwBgaUn8CQE
np4gkBEEeoJERpDoCTI9kUwnkvlEspRIoRMpQiJFTqRLiXQ5kc0nsoVEtoHI
lxL5BqJQThQaiFI5UWogyg0kKo1EFZGoChJNQqIpSBweiSMicYwknoTEM5JE
CpLISJIoSBIjSWEkU+lkqphMVZLpUjJdSebyyVwxmWsi86VkvoksVpLFJrJU
SZaayEoThUan0GQUmopCl1PoKopASBHIKAIzRSinCM0UmYoiM1PkKorcTFGZ
qTQ6laag0mAqXUmlw1SRmCpSUEUWqlhJFVuoCpiqsFCVMFVpocIWGl1Fo8M0
iYwmUdAkVppMRZNZaQqYprDSVDBNZaXBVrpUTpcq6VIbXa6iy210JUxX2ugq
mK6y0WEbg6lmMDUMpp3BUjNYWgbLwWBrGGwtg+1kqO0MtYOhsTM0TobWwdA6
GXYHw+5kOJxMjprJ0TE5LiZXw+TqmFw3U21nql1MjZ2pcTN1LqbOzbS7mHY3
0+Vm8dQsnp7F87AEWpZAzxIEWGoHS+1haR0sbYCl97D0AZbDw3IEWJ4Am69h
8w1svpct1LKFBrYwyNY42RovW+tka4Nsg5dtCLKdXrYzyPYGOTw1h2fk8Hwc
kY4jMnJEIY7axVH7ODoXRxfiGH0cY4jj8nFcIY4vxOVruHwTl+/ninVcsYkr
DnM1bq7Gz9W5ubow1+TnmsJct5/rDnP9YZ5Ez5MYeZIoT+3hqX08vYenj/KM
Pp4xyvP4eJ4ozxflSw18qYkvjfE1Xr7Gzzd4+YYY3+Tnm2J8r5/vjfH9MYFQ
KxCaBcKIQKYXyMwCWUKgDQi0EYE+INAnBOaIwJwQBCKCQEIQSQjlBqHcLJQn
hdqgUBsRGoJCQ1JojgjNSWEwIgwmhZGkSKwTiS0icVykMIoUFpEiJdKFRLq4
yBgSGVMiS1xkSYlCcVEoJYqnxEqTWGkRK9NiXVisi4tNYbEpLbbExZa0OBwX
h9PieFoi00tkVoksI1EYJQqrRJGT6KMSfUZijEqMOYk1I7HmJNGMJJqTZHJS
uUEqt0nlWanSJFXapMq81BCTGrJSU0xqykttWaktL41lpbG8NJuXqcwylVWm
Ksj0CZk+IzMnZOaCzJqRWQuyREaWKMgyBbnKLFfZ5Kqi3JCUG7Jyc1JuLspt
WbmtKE9m5cmiPFtUwBYFbFXAJYUxpTDmFJaUwlJSWHMKa0mRyilSJUWupIQt
StimhMtKU1ppyistaaWlrLTllbayMp1XpsvKfFkFW1WwTQVXVOaCylxUWQsq
a0VlK6psFVWhqCpUVMUKbCnBljJsLcHWCmwrw7YKXCrDpQpcrqjtDrXdpbZX
1Q6P2lFVu3xqV1Xt8ak9VbWvqrE7NXa3xl7TOL0aZ03j9mvcNY3Xr/HWNP6a
1uHUOgJaR13rDGqddW0gog3UtcGINljXRuo6l1vnCulcDZ07rHM3dKG4LtTQ
heO6cEMXb+g9Ab0nqvc09YGEPtDURzP6aFOfyOgTTX2mafAGDd6YwdsyBJOG
YMsQyxpiLUMya0i2DNmW0Rcy+qJGH2IMpYwhxBjNGaOIMZUzphBjDjH5wyZ/
zORvm8JpU7htiuVNsbYpnTel26Z82xxJmCNJc6RjThTMiY45WTQnO+ZC0Vzo
mIsdSzxliact8a4lVbKkupZ02ZLuWkplS6lrKXetmZw1U7BmetZcyZrrWQsV
a6FnLVWspZ610rNl87Zs0Zbt2/JlW75vK1Zsxb6tXLGV+7ZK3+5w2h1Vu2Ng
d9bszoHd5ba7qnbX0O6u2d1De3Vgrw7ttYG9NrQPhg5n3eEcODwBh6fq8Iwc
gbojMHJUB47qyFEfOOojx2Dk9Aad3prTO3YG687g2FkbOGtjZ33grI+dg7HL
3XC5hy5fyOWrunwTV6jhCk1c1aGrOnE1hq7GxDWcuP1ht7/m9k/d4YY7PHXX
hu7a1N0YuhtT93Dq8UU9vqrHN/MEmp7AyBNteqIzT3Xkqc48zZGnOfOMZl5/
zOuvef1zb7DlDY69sZY3NvfWxt7a3Nsae1tz73juCyG+0MQXRXzRma868VVn
PmTiQ2a+ycwfbvvDU3+s7Y/N/bWpvzb3t6f+9tw/nQciiUCkHogsAolmILEI
1EeB+iLQHAWai8BoEYwkg5F6MLIMJlvB5DJYHwfry2BrHGwtg+NlKJ4KxRuh
OBpKIaEUGmpMQg00hExCCBqaoOF4OhxvhOOrcLodTq/CjWm4sQq3p+H2Kjxd
RRKdSGIRSXYiyWWkvojUl5HOItJZRhbLaCYXzTSjmXU0h0Rz62hzFm2uo8gs
iqyjs3Usm49lW7HsJpZvx/KbWGsea21i7XmsvYnNN/FUN55C4+luPL2KN9B4
YxXvovHuKo6uEplCItNMZLaJQidR2Caai0Rzm+gsEp1tYrFNZovJbCuZ3SWL
nWRxl2wtk61dsrNMdnbJ5S6VK6VySCq3T5W6qdI+haApZJ/qoqnuPoXu0/ly
Ot9O5w/pcjddPqTbq3T7kO6u0t1DenXI5HqZ3DpT6GUK20xznWluM711prfN
rLfZfD+b32SL/Wxxl21tsq1dtr/J9nfZzS5X6uVK+xyyziH7XG+d6+1z632+
3M+XD/n2Jt8+5PubfP+Q3xwKxUqh2CkUj4VKr1A5FjrbQudY6G0LvWNheyxW
+sXKsdjZFTvHYn9X7B+Lu2OpXCmVu6XyqVTplSqnUndf6p5KvX2pdyrtT+VK
v1w5lbuHcvdU7h/K/VP5cKr0jpXeqdI/VvqnyvFUHQyrg1F1cK4OJ9XhuTqa
VUfn6mRWnZyrs3NtMKwNxrXBpTac1oaX2nheG19q03lteqnNL/XBqD4Y1wfX
+mhRH13r42V9fK0vlvXFtb68NoaTxnDaGGKNCdqYYI3pqjHFGuiqgWKNFdYc
zZqjRXN0a87Wzdmtudg2F7fmettc35rbW2s8b42XrfG9Nd+05vfWctda3lub
XWtzb+3uyGSGTFBk8kBma2T2QNA9gj6Q9R5ZP5D9oz2dt6er9vTZnm/a82d7
dWivnu3Nob15tg/PzmLZWWw7i1dnuessX53tsbN9dXbHzu7VOb666KqL7rvo
u7s6dFfv7v7U3b+7h1P38O6e3r31trfe99af3vbY2356+1Nv/+kdT73jp3f6
9De7/ubQ33z7u2N/9+0fTv3Dt3889Y/f/uk7GJ4Hw8tgdB6MroPxZTC+Ds6X
wfk6uFyHk/Nwgg2nl+EUG54vwzM2vGCj2Xk0u40W19HiNjpfR+fb6Hobzy/j
+X28vI6X9/HlOr7cx9f7ZHaezB4TFJugj8kZm5wfE+wxnV+m8+d0hU1Xz+kF
m16eU+w5W99m68fsfJudH7PbY765zzfP+eU+vzzn9+dieV0sX4vtbbF9La63
xfW1uL2Wu/ty91pe78vra3l/oSsMXb3R/QPdv1HsgWJv9PFeHZ6rw3uFPVfY
e/V8r7e39faz3j/W+8/69ljfPuvHZ7O7b3bfzeG5OXw39+fm/t08v9vja3v8
bG+v7e2zfX12x9fu+N3dX7v7d/f67k/v/emzf7z3j8/+/Tmc3ofT9/B8H57f
w/t7PH2Op+/x9Tm+vsfP9/T+nN7f0+d7vlzPF+x8+Z2vt/P1d8YeZ+x3vj3O
t9/58btc75fr74I9L9jvcn9e7r/L83e9va633/X+ut5/19cPe7yxxw97vrHn
D3v/bo/P7fG7vT631+/2+d2f3/vzd39976/f/ft7vD+P9+/x+T3f3+f79/z+
Xp/v6/N7fX/vz/f9+b2/v8/39x/UBlVV
"], 3 -> CompressedData["
1:eJwNkmdX4mAYRDehg9IFBEGxV6xgQbGAimDFhkqRIlXpkPz8vR9cz3HzzjNz
Z/zFdqoo/vv3L80/Sn4LokLJj0oQlWpBVGkFUa0VFEqNoFDpBIVGJyjVekGp
0QsqrUFQ6QyCWjsmqPVjgkY3Lmj044LWMCboDOOCfmxcMIyNI2dEziQqjCYk
zaLSaEbWKqpMVqTtotpsF7VWu2g0zYpG86xoss6KZvusaLXPctbCcwunbUjY
OD+h0FgmFDrbBHJzCqNlTmGyzSksE3MK28Qc1hyccGDPyVOnUu9wcm4eiXml
2TGvtDjnlQ7nPNZdWHBhfxLpSZXBNYmdBU4sqKyuBZVtckHlmlwgmhuLbuJN
IT2lHnNPYXeRE4tqu3tR7ZhaVLunFonuwZqH+F5OezXjHi82l7CwpJnwLGmc
3iWNx7sEGh+nfcj6iLyMhWXkl7Uu37LW7VsG2zSWppGbJuIK1laQXdFNTq/o
PNMrIJ3BygxnZoi2iqVVzq3qp2ZW9d6ZVXD7OeFHxk+kNU6tIbdm8PnXDNP+
NZ77ibDO+XVk1vl0fWzGv47dDU5uILvB0w0+26COAIgDVLIJwk1Qb4Fxyzgb
2DTOBbaM85tbxsDmFnVtg26bGnbAt8OzbZ7tmBa2d0yB7R2q3AXZLvj3wbaP
3C5y++bF3X3z5u4+1e2Bao9qDsB1wJk9zhxYlvYOLFt7B8wgCKogtRyC65Bz
Qc4dWpeDh9bt4CG1h0AVorIjcB1hI4SNI9tK6Mi2EzqipmMQH2MjiI1jpI7t
u8FjajkB7QnnQ5w/QeJkYi90wjzCoA1T7Sl4T7EdxvapYzV86tgPn1LlGcjP
sBvG7hmfnjkPwmfMJQLyCFWeg/0cuxHsnrvWIueuw8g5FV5QxQU2I9i84NOL
yaPIBfOJUkmU+i+p5RK7Uexeutejl+7j6CWziVFPjPqvqOgK2zFsX3k2Ylee
k9gV1V9T5TV2o9i9Rup66jR6zRzi1BnHbgy7cSTi3rNYnCncUPsNNi+xecPJ
G9/55Q3zSFB9AptX2ExwKjF9cZVgHknmkORMnDNJJJMz1/EkMglkkjxJ+m8S
SWZxS/W31HtLRbfgvmUmd0zhjkrvqOUO1HfM5p7676n4HrT3YLxnKg9U+kBt
D2B7ANED83ikrkfQP4LkkXiPTOKJqp7A/gSGJ6I9MYMUlaZAnQJbilgpqn+m
zmcwP4PqmUjP1PdCVS8gegHHC3FeqOaVGl7B8ErkVyK9gv0NhG9geSPuGxHf
QP0OvneQvBP/ncjvTD9N5DQR08z8g+gfRP0I3KY/AnfpD2KmmfcnOD6J+8mn
n5v36U8m/QWOL+J/8fSLz76I/8GUM2DLgCGDVGb74SPDfLNgy4Ili3SWz7JM
NwfaHHg+wZNDPrf7+Jljunnw5kH0BaI8J/J7T1958GTAk0M6F0xlcqDJgiaP
bD70nM0z6W9q+AbzNza/kf1mzgVqKYC5gM0CkgUmXKSaIpiLWCwiW2S+Jaoq
gbmExRLSJTB/g7mAZCH88l1gwmXqK1NNGbtlrJSZ7Q/1/VDND1Z/sPNDFUWq
KHGiFHktlphwhcor1FXBWgXZCvOtUnmV+qpYq3KmynRrVF6jwhrWasjUmG2d
yutUWsdaHdk6tZaptYKVSvStXKHSHyqtYqMae/+pUncNizU+q1FzHWt1Pqkz
9QZTaTCFBlYaSDSYQAMLDZ43mH6T2TSZSRMLTWSazKPJ6SYyTZ41+bzJLH6Z
wC/V/lLZL3X8MpM/JvBHtX/U9Uclf0ykxSRaVNECfQuMLabQpvo22NtgboOo
TeUdquqAtAOeDrE61N2lqi5Iu+DpEq1L5T2q6oG9B54eEXvU3qeqPtj74OkT
tU9VAxAPQDog5oB4A2oYgnMIviHRhkQagm4EohEYRkQdEW8EPglUEjgkIkvE
lYj7R9wW8Vrp378WsdvEbPPnNvE7xOvw3x1id4nZ5bMuSHpE7PFpDxR9ovZ5
0idijyc9YvX5vA+SAZEHSAyIOeD5ACRD4g15PiTSkKdDkIyIO+L5CBQSMSUk
JOKNeD4iosRziWgjno6IJ/FUIpLEJxJ/lrAuY1nGqowtGRsyVmVsyViRsSBz
XuaszEmZUzLSMmdkpGVkZSRl5GTk5P83BzlV
"]|>, "SimplexVertexIndices" -> CompressedData["
1:eJwtlflDEl0UhsUl1xQGLVMY1DJNDfc0GXAJNQUx1xJwDwZcABfk/vnf89r3
g4/vvXPumTtnY/CqvH9VX1dXd9FQV9fEf099Q6MPNPmBDzS+8QIve00tFrDY
e9PSAToCwAtaOmxggY4A8PrCwHqFAwLA52dpvcJmGQANjc0+T0NTq9/T0NyK
auVtjW/aAgCnjc1tQeADbQHg9UVAAPiCIACaWlrbBcvT1Mqt3rRxoebWt0HA
seY2FBbjwALtXLKl3UZZoLX9bQiEUG+DKJ8/CoLA8rPnD72CZRC0deAK70FP
ewfH8ARsTDp0lv0EsEEwBGxACCIeQuB4uDIIA0IQ9XB5EAa8JwbCwJayHRAG
vFuIgjDgSxMe4gUigPuACLBlZ4diKAdwIOHhPQZEgRMDUcApEAWYGQ9mhhx3
+shxl7++obML1eXz1zd2en31TV2WX+m1gdUt2Eq0A2zg7Ra0tKS4tFLu1OMk
DIaAV8qLwiewXsHSa3UPCQ4YCivlPUp5jy7wURf4SLn1fKQC3gWoANDc9j5I
BYC2d+/HQAC8D46pIMZ0209UxadII7YCClsB9e4fxkAAcCpCzYxFVDNWU0u7
1duE8AP/hybEMOgF/g+gF3DxYeLQZysOoBvV0RdwgO0Qh8+O7viZYKCwcN50
972CZR97FGJ/UB8ZVTWCnn7Qj/L1jET1VSMUN6qnH/SjdLNx3Qz02uN67WiL
1fsP47rAqK48riuDD6FxvSKkGEZb/T1fwIfQF2Gc0mXZ0w+wACxVxAMq4gHC
NzCmSh5UJQ/q62NyHFMIBBRxEFC9Ur1S2I6r4gflaZBg2BOCI58JymACDAAs
wACwpexB9gaAbvtV57/q/FflPawsTqpmJlUzk51sTXWyBcKTU6qKsDIxrTqa
Vh1Nd7E108UWCE/P6HxKZZCSEwFFqc2CWUellgSzSTUjmAXdn3lA7hbAQoTC
AawcLytHt0h6hyY58WlyIeXlYcr7eZan7KdBKq1uFqQc9iZnFwSpBfawBXqw
IDvOp1XYc2Auqg9ChVE9I4AyWASLEaoWsNpTVcRBHLUY2dPEYBlhSWzmFJuU
79PUIliMpHwjc5zAUxxgEtZTzDIgBeaiGU0bgeXU3CJYRM3JM0DJM0BFwaLs
eGNGUd9Vaewq9AKKknQU3Hmre3QeNQuo0JgqFAx/B6MAs30Q29dY21faktbQ
9DyYBcPT33ctbHet0fnv+wBjTu1bmGXBblaDUNAyxnJ6/rvAkqNZi9cmLY5m
rXmZcD5rfZcdTrIWb8wq4N9oim9Rog7ojDV1RgzEUMNLqC9LqCWWtMcBWDvQ
2AUxFFW2o2SBmW9gDlB0u/7hmSWwFNv1f/m2dAA4i6cDVeOun1OnYPdUORa0
jMZOFb5T/8y3JYE9nJz6uZnAEk8gCpb08iUZL8VYcp9Ttb6jgl3WMFtW1S6r
cFY01lZUPStKwqqSsKr4r+pL19SgjmbRj77ABMDJeh9b632s1tWMcU2HuIZP
XCNio58tEI1vaEQkNDATcnKs5j7Wj9BxYGBsM0GbA1rmly71S68Ay4Dr5UEC
LG+CTRRvOw5M/NgEmzigK/L6AuD8AsuA36h8ACfCMUiA5R+bAnsczQc4mtfs
SOjeCd07oSkCxn6Cr4CI7AVHVuJ7Coury4OVn+An6mscE0K1p4Zy9RMKZAzc
IO7c4EocY8xcjbqEfmAT9uD4FpgAhG9fYQarKGJdAAmwugW2UAT32J5Y3wJb
iWP9LhfUAGD9FccFxbBg46Rgr65vCSgOFGwOFHjtdoKPBKTjgJIEpLKoq4C1
bbCNIk+/FQewsQ22UVGZUC9FJVDQcoMlFVUMrW1sCyiOggTgaDHE0SJJ/Zng
S7cTmjE7mne/NFT2VEz7JPUwT0gPXWUWHILlTfZWfrLH0UMSzRLhjiFcYnNU
4N5HRQUIHIHVLfbWttnjPbfg6FZBA0eArwJHgAO34xy4VZkeK22/Ndb+MID/
pBnAgDtmwlM7f0AK0HgnzI6TLLMDzOycnNKCgPEHdgCj2GgQGs3tTDiSRjFj
jCZ4NuykUXQpyABGyWk4lkUl/5xkACeSJ3jhFUBnkzqRlHFSdjuy25FJSsbc
4lRD6kyBTOvH4GwWcaaGP1fDn2sAZzR7Mwoz2Muc67bnuu25xtqZxtqZZsK5
fkjytMxFXr8mFwuRNAp/eZoH9YulCvtSw/tSji+VtiuNxCuNxCsNlWsNlWsN
lWu1m5FPo0nvqhVQGbB8eJFXU7hyBw4B13OVd6PICZikdJaXuUAPLi6fQR5c
uiD/D0ZXcSOHenqop4d6Sn08qzOMBnWBJKBI9F/6/2+e/gfr+38LdAug60Ee
EyJ+phhW9OHg7C/4iyJKQgFoj6MVBycFksqDdLZi+FKAhXHYrzj8GXWL0XQt
kndUfCNX1BAoKh0uyIEcy40DHrBvlKIc4MEBORJqgL2DTA51WgQ5wL6JYoZy
UeybKJ5qUf6MElOgPQA5KdIjgJI3KrqyMlZWnsAVIHcFZawYO7q6roICuC5W
1VBVKrRsYliUiSEKszLfguJoNcZ+NcZWNVb4H4bWzxXVUC797xbjv7mW2vdG
7XujEXujHr6RxY0G0q2mw61a+kaZqMmipn1wA3AisIcZ0F5eyzxfTtqAPlot
XQM1Q0OlM8JdEmHAnVFrlUHZqL9Q2Ttwx5IM3gFMsDDJ7Ct4oHa7V7vdq1vu
1XMlirNkVJwVUALkPJUuAWrwAZSA+8CyBC4uS88UbAWUABagBPJu5RUm5VZY
ApMqSQGjvi6r3SqqhQdV94MK4kE1+KhkPaoQH1WIjyrER1VKDuRq9HHuSakE
uSeWRZADCu6z5l1VVftCmF9qhBkUbsENUJ5qity9InfP596X/iBK2jLaMgpG
maiUzckdkIVR+CqEr2JkC4iG7vOgoIHcg9HNjI4KLPmWWib3wJ4r3BMrOXlU
lT1SZY9G32dIgoCSuye5e1L5PeHzyej7DIWIKkrdS2Fh5KQqs6r68EUBeuFA
zSgENYUe9cySh0ZxMPmb55caaWKJMMqJIVc1o3jVVNioKsvb6ktN3o18msJj
FbBl9DJTfMJEWTT/AdA2/WM=
"], "AffineSpaceBasis" -> {{0.3090169943749474, -0.8090169943749476, 0., -0.5000000000000001}, {
0.17841104488654494`, -0.4670861794813579, 0., 0.8660254037844386}, {0.12615565967785344`, 0.0481871741237754, -0.990839414729355, 0.}, {0.9256147934109582,
0.3535533905932738, 0.13504537836886318`, 0.}}, "NullSpaceNormals" -> {}, "NullSpaceBounds" -> {}, "HalfSpaceNormals" -> CompressedData["
1:eJyFmztvnVkVhi1EiYTEP6CdngaKr0YaofFxkEaiQ4KWngZIMvwH4tuIf0DF
KIy9nQsmts85tpPMieM4TsbDHAkkeoopiMh+1qf17LPBRT45y/u2Lu+67LW/
//NfTX7xrbW1tY/f/fPtd9/b9z785x93/lW++PUPvvu9f5+Ui/q9qt/Jzy5/
+PGH/yizH/3mlzufLspZ/Z7W78433/nzxk9uhq3337Jdf59+82Tvgx8/CPo9
0Q/f04c6D/ThdV13/t//Xw4aPzyu89b1evTB6xzWddbqz9335x7qOYfz+n1a
v5Uv7GfYrPMx/tZ7vsT+j+p3Wr8T0dnfZZ2P803Td8F+gm+sM8/zF36/U/dZ
5TYgx5fa94v6+3Edx/ozrc/+4B/n4P85P3T4eFD5DJ35NsSHmb6M97hS57ur
83EOzjeTXB/UccgPvte/L1Od33Jd1Hnh+0n9uzX9wDf+vn5L5VNh/RPJjS/z
v6rjT7P+lbsar/PF/GfSO+wUvnO+58mu2Ed7fvSH8djZVdafYv49yHYZds74
h1UupsNH6V3oN+ts6f8v0n6W2EfwP3Co0isfwy52pN+zLJ+wt4+ynAp82q3j
P6lygL/si/Mgx88rfxgvvcCOg34o/OT8ld/F+Lop+nHlN3TkVvUZfA/+i7/l
WnTOz98Z52ZJL0Z8gi7cCD6BX4uMW2UhuvhW0DfjB+cEj5DTevVj/N21cLbq
SeGc5/JvU/HN9O3M95AD9PotT+q+NhO/0c9l7I8f6z9+96u6z1vZTsN/G6ds
P29l5+wfvns8cr2p49g/8j3P9hN6gPxmkhvzI7+nmR7ry7+FftjOlxnfwIWS
/eyi1HMHPzg/cQ3+hP3/tNKfi6+c/7b2h16zT/a/r3Ozn57/q/obdga9zhN4
gX4Jv8GtoIN7zDcVf6x3Ve4Njlf95f+NTxFvQT/J/I/4Brr0q/EDyOeF9NLy
m0tu2MlkdfwU+oj8yur4pThONE5BZ9/C/6CjV0V6gH6wr33tYy7572XcC/7D
V/QY/bd+oKfox24eH3xB/i90bvTu9Up7C347Txi+TPHXsvEj93Uu9rub8Hc8
1xvhN3HTRDgP/W+KTxyHHCo+2Uz7i/gkxuV4YWm8lJ9fBn8V35Sef2Q98Ap8
3c77CrzGbxG/kdfBf/wPfgN/A/3parsp2AXnFW6zz5gfOuPZH/rC794f5/p7
pbO/+er9EVeUhzkOslwDj39f18Nu8f/HwqtNjf86x0HBH+jXkiv6yX7PtF/s
4lznQZ7Mgz+7krzQmy3xG7sEX04lrxonYM+xTsaZpeOGiIem0hfLG33Af3v9
itPMN3TiwPidc6MPU+kD49kP8Z31Zbaav8ONzoV+gysVd8o96ZXi8uK4+zDH
3SHvTdn1tCNP6g1z8d/yRp6HOU4IOvYFX/8iv8O+oN9f7XcCB9Ab4XKcA/y/
Fh6w77fp3Iuwp3mWU9CR56Xs4EL4wX7AAeR9O9sDeVgxjuHf4OfmSrsY96vz
DN7Ps7rPG8Vbzu9q/hZxGbhxpLxCeVTwueJH1Acc/yvub/If7Aq6/EnMD53z
c17o5P/w7WH2s0HHXg8y3pIXB39cz3kpfKA+t1QdaEPxruW3kfkX+zc+7GR8
GBSngssR78xkJ9Msl/Az+J/rvO+wX/TT8R7nxr6dR6B3i2wfkafKvm3/Q6++
eyY7yn5hEXLu0Q8lV+QGP7Br8w2/wXkfKW5zXk28bBxG/15kPQ+8qv4h6nes
l+OzJXkf88R5r2TfnBs7Q7/Qt1x/G/3QVbLXRRN3yg6avBu68sXIa6B/Vvl0
Ijr8Pxe+qz4X+wPHoROXnGT64LoV8j5O8l326kZxPvSar+QwbMk+c/wY+BT6
c9Spq/E9znnAYD+Y8+cxn3X8cim9Yv4s77Gu5njAOMb81BGxT+MAeHou+nqO
x2P+9ZwHFtc5ke+Z4sPwY/X/GQ9+OF+6Jf9zJjp28VXiR+hJcTx1Kbv2/M+E
38yT475F1H2cd95XHP2J6OAO4zcU37sONsnxaeD8lXAFOwfHr1frV5yf+zDo
jru3Ml4Gvxm33aE/URzv+Ocq4dkop62sR3E+5OM49jrjSTHerM67xzyEedCf
aUdPmX+iuNJ05EgcDv1YeuI6jupF8DfiDq9ju3+tc8L3Tr0h/t51af4ePM76
P8Y5lwmHRj3dkJ6Cty87esp6ttu59OFQfnxb+vZo9f1Q8GEuu1K+F3ZiPXyt
czoOQD/5LnRO5GY9dJ0J/yv/ij8qjtPt342nM9GfCs+o+/ve9Y7iyAvp8URx
MnpOnOL4x/PgD/D/2f7GPGdP+Q3j7+Z4NfzogeJFz+s8aJb5GfPb3uTHY/9v
szx1L71UHr7Qfkd/JL2M9dFT38dMhIOq25k/EWdbvs73+cl5tes5YzxPHOG6
N3Ts5aX0Bxz3fZHrOOAGccpr8Y/zQ3ddD74iJ/JIx0nC1cjj4TvrOs+Ff717
QPglP+m6RtMP4bqn5BL6JdyIe0rhYuQn7O8k7394lvT0Xb6ScS7uNXTP0NQ/
fA8I/TLLNfJW4jflz00d4izbRZPfPct6P4CXpwlv2j6AC9HBQ+qq9ONsZ77G
+fBHqk/E/NQx3UfwNp+77HborI/cVc8JfzMVXXFP8A2663AdvIvxwrPG7hwv
GTfQd+Tm/gHL2/th/mv9PXjs+ED195DX49XxQdBdB5Jdxnrs543yM87H+FyX
b+MLy+tAcXg+/9iP4LjC+YzvXRX/GB+j34v45I7qE45zJxm/Iz5/me2wUPc4
6PifbPdtH9dnOR5q6H/q2Ne15OI+uNDTuu/dJIewv+FJXRf6hsZPsz/SPhbq
F2vsU/n9MvBpTT8T2a/jMfcJQVe/VtMHmO9pG/yNuon7JPk+Fv5tZXsa/lrl
o/uH4DN6yzks58fSm03JUX0csf5p8pOjXVpOF8Iz6Oj9qcYjh+xPxvgM/4be
L2Q39HkRNzn+uJPpUR92Pyv+yX13jvedH6C/5FkeX+vL0Z+B/wFvnCe4vgvf
wAPyd9/TWq4T4aXrG9SFON+XivsVT8Y9sfgQ53V9SfFkyJ3947/uZT1v7vG2
REf/FU839u16Lfxz/m78Uh3O/In4Drrxi/jI/Zy9+sx61v+S6zpNP2f5UvOz
/6dpvUVTT2Z/5C29Pifq0chRcU7IH5zA/vB3z/XF/vDT5FPuE3T8i793f5Hz
Acvd8bz6p5v6MuPY7y3F2/i9fK8U/eFxb3WV9TrsC/tw36j1H73O+cTID/qL
kCd4xfrwDzwl32D9K+Gd8xHFOaHvyEv9K8PX8j/GQ/AOfw8defv+Cb1Wn3bk
E8QP5I26N44+IeMffuVsNZ+Mj/HdEP5dSw+Jt4V/sX/idd8XK+91vBw4vtOh
P5J9nkmOrHvQwVHbsfs1XT+zXaH3TxT3K05p+g1yPDb2I7B/31vlOGOMn26S
no799OdZvs17Fe4VbQ/Kr0O+HfyKvP7havzq1Q0HxxH8gDecy/ED83P/hT1d
yF6rPQef1I8adUTJfVCfclPXZH32d57xsMqvif+a/B/+H+X9N+8NsGful6GT
L3ifnfg26FtZrwOn4c9utot4l/JK55DfiXPmfHDsp8UuiCfy+4Vl43/wc8pL
Iv7zuwv7y/2cxw6533TsR2F+/HGtF8V9PPoC/jPO+RzrEi9wPscbc/HJ8Zbw
NPi7yPYQduw+cOPsRbL75v4r6t7Ug8C7XenVm6yfeg8w9qN16M4XunGq+6V7
/ezwzfEQONh7zwJd/e7Nuwn4cyb9dd+QcZ68yn4q7u3rfOgN/s95IOdz38ZF
sp/RD9iP2E/ke+r23R9+z/3g6IfzTL+7Ih5CT92P3usnd182fPK7Ht9T+91O
p1/R9YyI810n2M9yjThmR+czTrn/g32gl9j/nvIMxv9O+MB9IXGm7dDvb5x/
q97QvGvaz/uI/bk/yfrrezXsGnrJuOe+L/g3uG9xI/PPehDy8ftF5f1hJ+7X
ZfyJ9Exxbdg/43ZkN8h9f7X9R//tnuzffTv4F8vF7wyQK3kleg/esm/OA27A
H7+n6tR/G9x0nJT1brxfZP7cTz76V9UBwy4uhC/uB+zgS+TP6ssPu+/Uf5v8
xvddu2n/3XdtxfdZrov4Por+Wvfrsj79szPND/9eZD1s+n2xpw3Nn9+bRnwU
9D9key3Ky4Ou+76mX0f5d1Nn/DzHX8XvhZwnEH/b/8CH55LbRP6H8x7LPlT/
ifc3rtOSxxi3cx1g3Odc4zO/R/33/b/rJq4rHyjO97s15OI6ufx87M84+Crr
bRNH6/3P4HgB/jMefd7ryBdcAa+/kHyxa8dxtv9OvcJ9mY4Dwt+gP+rTVh1o
fPfmOiD6c9DBR/h0Lf1gfdXzw+/oXcXgvlP25/sS5w3I40j+CVxCntwXQ9e7
EfenNHljzz8pD9S79vb9meN/34v43tL7cVyX+bagLhD4C/2e+Ag+qo8x7q9r
fBbv1ZhfeVjQeeeve8HwT7rHKq4/HelexvewNxkvmn7S9ZwXlU/r31Gn8Pl8
72K9AP/RC+wQOv4LHCNvVX9w1D2fZTwOv3yc+dq8e7J8qZv05HuR7bCRL/Tf
5rprjIefzE993v2c6Me5cMT1R3DuSPEo/N2T3bouznr5vqd9r2P8dv0S/eT3
U8U9HykeZ3/4c/dzu27de2/0IOcXg+pYERcp3x77oOQn5Sd6+hf8Q1+ou8mv
ue9R9/vL4ndZR/J38AFcwU7xt+43g66+JfdbRF31/9AH9UvG+wL+Xu8C4t2H
60KMh44/Xf/f45t+Q+j4W+sh8nfejp0a/3vj3a8H/7eT/XX7h4I/eq8T4w+y
Xfbo6t8f47vV9/8j3e9+ev79P+x+3YE=
"], "HalfSpaceBounds" -> CompressedData["
1:eJytlz1uwzAMRtXepCfpBTp1ylygc65gu7Zzhw4derwAvUOXePmAh0cGmQhK
osTfj9TLx/n982mMcXoeY/l+u/7+/L2uN/oVdLvRJdbXWCd+K96f/Ap0AXrI
z8Ef+1PwM8iTnfl+2pH2kp+qNOWJJ/+TftW4UTzIbxZfemcv2mt2Ut5QfCy/
unGfm/d140h1RfdvzXMkZ3pX84nyg/LzWJ9ED6o7wi16z/I7/WJ1tcN5qxei
iQ90r8kR/hFOJa7aebKrGj+rW/J/+rtbz6af6WN1QbSKvyZH65QnuV/FqWo/
6fZt87fx1fVL8d579aLzlreE99ZnTa6rt8XF6svwnfLS6i/xh/DZ5rK9qS/h
H+FhtT5sDjZ/VPuq5XEXB6tzVdUvNj8TfdSc8ihKuGrnzF+JD/mfoT5B/qn2
Iaqz7lxe3Sfe6o5wwfbpvW7/ruKd3Zvy+Y81/9g5eqc7n1j9WN5X9bP8onqx
/CG8meJ8NY7dOd7s7+ZrVz/yF71j+GpzU/L5T+7Og0n/ARg2Is8=
"]|>];
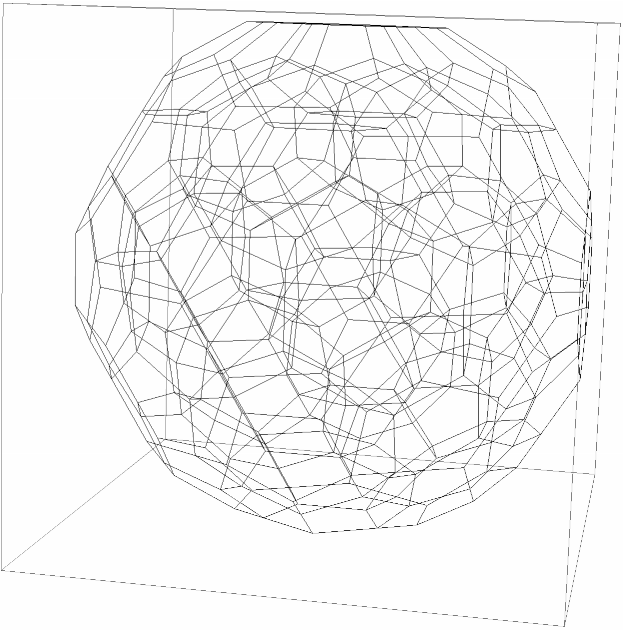
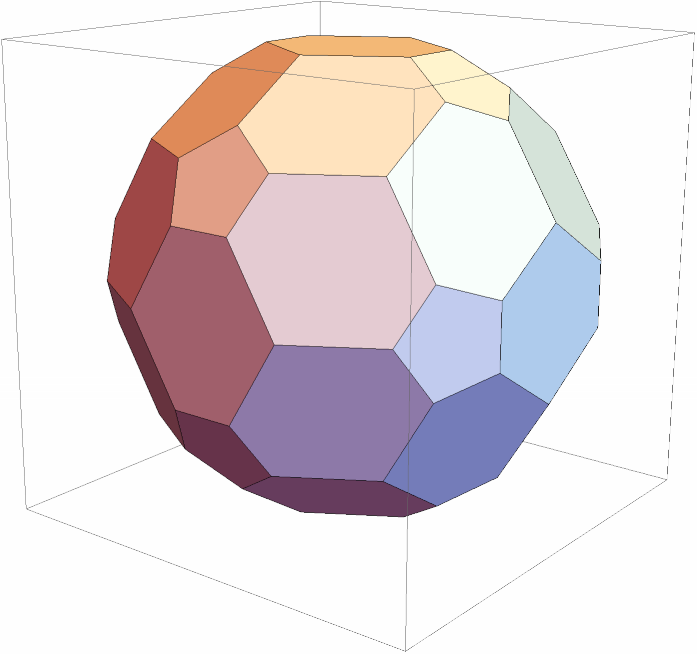
c120Polytope = c600Polytope // ConvexPolytopeDual;
c120Polytope["FaceCounts"] // Print;
{c120Polytope // Line} // Graphics3D](https://www.wolframcloud.com/obj/resourcesystem/images/703/703e94b5-7e08-4c0f-ac24-9023cf425fe2/3a37a4c888f0c8b5.png)
![Manipulate[
Graphics3D[
{
c120Polytope["Slice", {0, 0, 0, 1}, sliceValue] // Polygon,
c120Polytope // Line
}
, Boxed -> False
, PlotRange -> 1
, ImageSize -> 400
]
, {{sliceValue, 0.6}, -1, 1}
, TrackedSymbols :> {sliceValue}
]](https://www.wolframcloud.com/obj/resourcesystem/images/703/703e94b5-7e08-4c0f-ac24-9023cf425fe2/79c4a141a7477b64.png)