Wolfram Neural Net Repository

Immediate Computable Access to Neural Net Models

YOLO V8 Segment Trained on MS-COCO Data

Detect, segment and localize objects in an image

YOLO (You Only Look Once) Version 8 by Ultralytics is the latest version of the YOLO models. Just like its predecessor, YOLO Version 5, YOLO Version 8 is an anchor-free model that was trained with mosaic augmentation. It features the use of new "C2f" blocks, which employ additional dense connections between bottleneck modules. Although YOLO models are historically object detection models, these models perform both object detection and segmentation at the same time.

Training Set Information

Model Information

Examples

Resource retrieval

Get the pre-trained net:

In[1]:=
NetModel["YOLO V8 Segment Trained on MS-COCO Data"]
Out[1]=

NetModel parameters

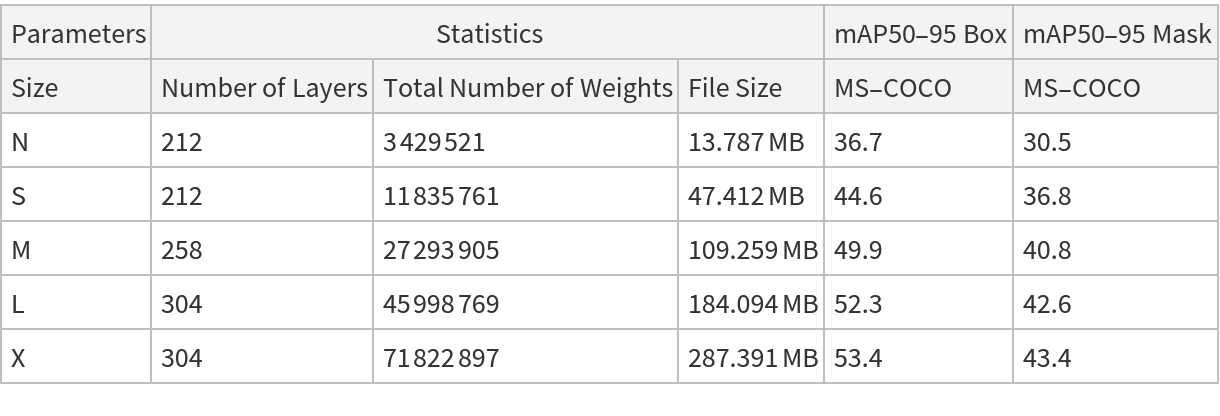
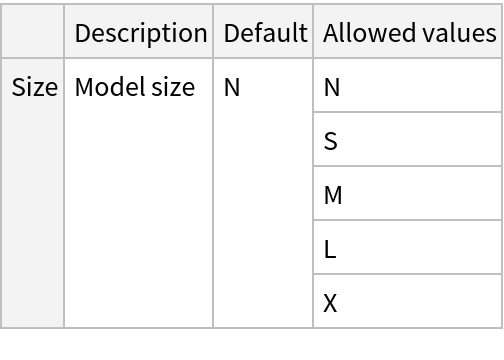
This model consists of a family of individual nets, each identified by a specific parameter combination. Inspect the available parameters:

In[2]:=
NetModel["YOLO V8 Segment Trained on MS-COCO Data", "ParametersInformation"]
Out[2]=

Pick a non-default net by specifying the parameters:

In[3]:=
NetModel[{"YOLO V8 Segment Trained on MS-COCO Data", "Size" -> "L"}]
Out[3]=

Pick a non-default uninitialized net:

In[4]:=
NetModel[{"YOLO V8 Segment Trained on MS-COCO Data", "Size" -> "L"}, "UninitializedEvaluationNet"]
Out[4]=

Evaluation function

Write an evaluation function to scale the result to the input image size and suppress the least probable detections:

In[5]:=
labels = {"person", "bicycle", "car", "motorcycle", "airplane", "bus", "train", "truck", "boat", "traffic light", "fire hydrant", "stop sign", "parking meter", "bench", "bird", "cat", "dog", "horse", "sheep", "cow", "elephant", "bear", "zebra", "giraffe", "backpack", "umbrella", "handbag", "tie", "suitcase", "frisbee", "skis", "snowboard", "sports ball", "kite", "baseball bat", "baseball glove", "skateboard", "surfboard", "tennis racket", "bottle", "wine glass", "cup", "fork", "knife", "spoon", "bowl", "banana", "apple", "sandwich", "orange", "broccoli", "carrot", "hot dog", "pizza", "donut", "cake", "chair", "couch", "potted plant", "bed", "dining table", "toilet", "tv", "laptop", "mouse", "remote", "keyboard", "cell phone", "microwave", "oven", "toaster", "sink", "refrigerator", "book", "clock", "vase", "scissors", "teddy bear", "hair drier", "toothbrush"};
In[6]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/d8f9c7a2-8d27-4346-8fe4-da28a08c83a2"]

Basic usage

Obtain the detected bounding boxes with their corresponding classes and confidences for a given image:

In[7]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/2dff7112-edaf-4981-9801-4a254b705432"]
In[8]:=
detection = netevaluate[NetModel["YOLO V8 Segment Trained on MS-COCO Data"], testImage];

The model's output is an Association containing the detected "Boxes", "Classes" and "Masks":

In[9]:=
Keys[detection]
Out[9]=

The "Boxes" key is a list of Rectangle expressions corresponding to the bounding boxes of the detected objects:

In[10]:=
detection["Boxes"]
Out[10]=

The "Classes" key contains the classes of the detected objects:

In[11]:=
detection["Classes"]
Out[11]=

The "Masks" key contains segmentation masks for the detected objects:

In[12]:=
detection["Masks"]
Out[12]=

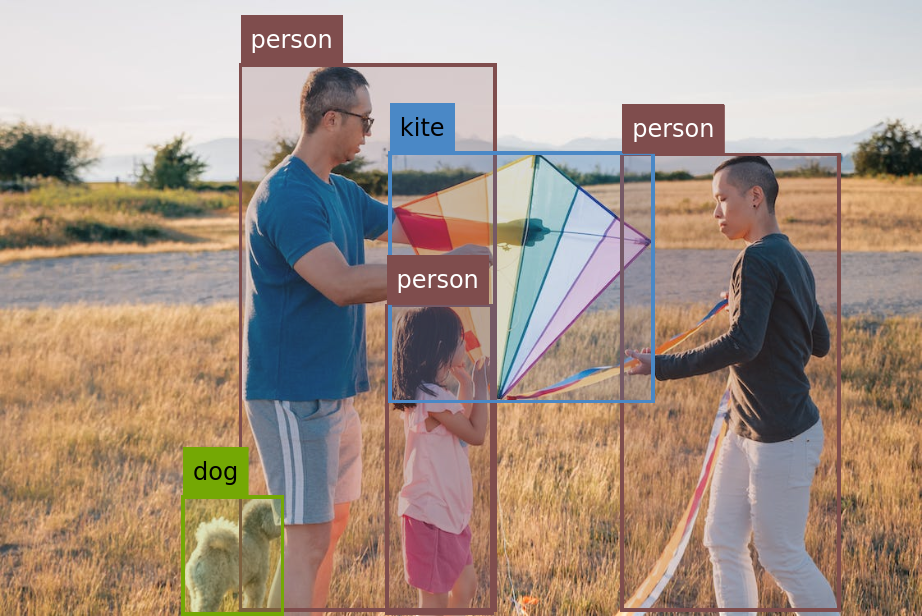
Visualize the boxes labeled with their assigned classes:

In[13]:=
HighlightImage[testImage, GroupBy[Thread[detection["Classes"] -> detection["Boxes"]], First -> Last]]
Out[13]=

Visualize the masks labeled with their assigned classes:

In[14]:=
HighlightImage[testImage, GroupBy[Thread[detection["Classes"] -> detection["Masks"]], First -> Last]]
Out[14]=

Network result

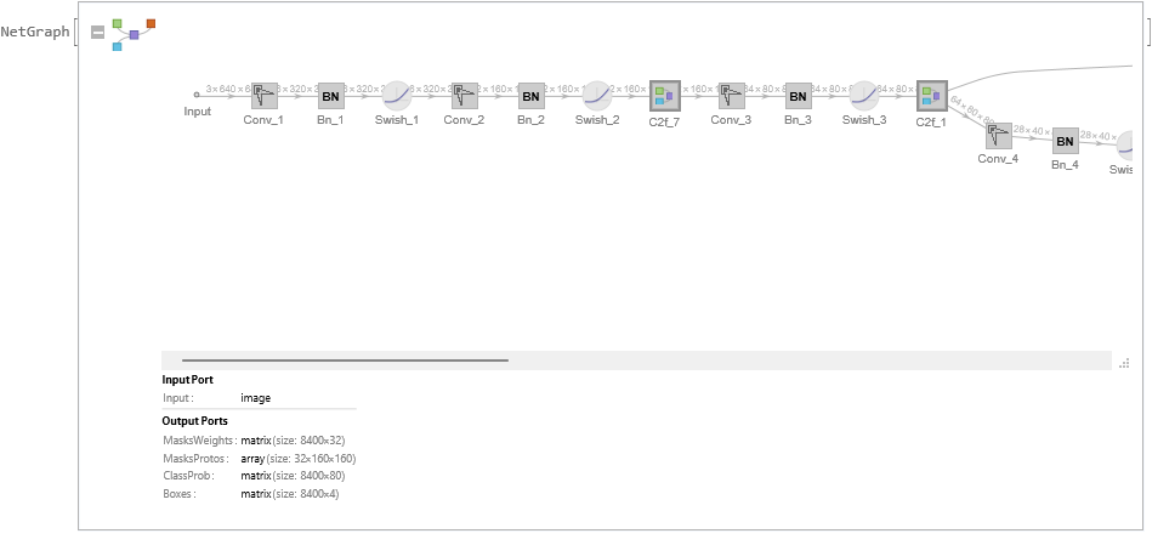
The network computes eight thousand four hundred bounding boxes, the probability that the objects in each box are of any given class, 32 160x160 prototyped segmentation masks and mask weights for each bounding box:

In[15]:=
res = NetModel["YOLO V8 Segment Trained on MS-COCO Data"][testImage];
In[16]:=
Dimensions /@ res
Out[16]=

Visualize prototyped masks:

In[17]:=
GraphicsGrid[Partition[Map[ArrayPlot, res["MasksProtos"]], 8], ImageSize -> {1000, 500}]
Out[17]=

Every box is then assigned a mask, computed by taking linear combinations of the prototyped masks with the associated weights. Values are normalized to lie between 0 and 1 with a LogisticSigmoid:

In[18]:=
masks = LogisticSigmoid[res["MasksWeights"] . res["MasksProtos"]]; Dimensions[masks]
Out[19]=

Filter out masks whose detection probabilities are small and visualize the others:

In[20]:=
isDetection = UnitStep[Max /@ res["ClassProb"] - 0.45]; probableMasks = Pick[masks, isDetection, 1]; GraphicsGrid[Partition[Map[ArrayPlot, probableMasks], 11], ImageSize -> {1000, 400}]
Out[22]=

Scale the boxes and apply non-maximum suppression for the final reduction. Use the result to filter the masks and visualize them:

In[23]:=
{probableClasses, probableBoxes} = Map[Pick[#, isDetection, 1] &, {res["ClassProb"], res["Boxes"]}]; {w, h} = ImageDimensions[testImage]; imgSize = 640; max = Max[{w, h}]; scale = max/imgSize; {padx, pady} = imgSize*(1 - {w, h}/max)/2; {probableRectangles, probableBoxes} = Transpose@Apply[ Function[ x1 = Clip[Floor[scale*(#1 - #3/2 - padx)], {1, w}]; y1 = Clip[Floor[scale*(imgSize - #2 - #4/2 - pady)], {1, h}]; x2 = Clip[Floor[scale*(#1 + #3/2 - padx)], {1, w}]; y2 = Clip[Floor[scale*(imgSize - #2 + #4/2 - pady)], {1, h}]; { Rectangle[{x1, y1}, {x2, y2}], {{x1, Clip[Floor[scale*(#2 - #4/2 - pady)], {1, h}]}, {x2, Clip[Floor[scale*(#2 + #4/2 - pady)], {1, h}]}} } ], probableBoxes, 2 ]; nms = ResourceFunction["NonMaximumSuppression"][ probableRectangles -> Max /@ probableClasses, "Index", MaxOverlapFraction -> 0.45]; nmsMasks = probableMasks[[nms]]; GraphicsRow[Map[ArrayPlot, nmsMasks], ImageSize -> {1000, 200}]
Out[32]=

Remove the padding from the masks, scale them to the original image size, binarize them and use the scaled boxes to isolate the region of interest:

In[33]:=
nmsRectangles = probableRectangles[[nms]]; {w, h} = ImageDimensions[testImage]; {mh, mw} = {160, 160}; gain = Min[{mh, mw}/{w, h}]; pad = ({mw, mh} - {w, h}*gain)/2; {left, top} = Clip[Floor[pad], {1, mh}]; {right, bottom} = Clip[Floor[{mw, mh} - pad], {1, mh}]; croppedMasks = nmsMasks[[All, top ;; bottom, left ;; right]]; resampledMasks = ArrayResample[croppedMasks, {Length[croppedMasks], h, w}, Resampling -> "Linear"]; MapThread[ HighlightImage[ Image[#1, Interleaving -> False], #2] &, {resampledMasks, nmsRectangles}]
Out[42]=

Remove any detections outside the boxes:

In[43]:=
nmsBoxes = Part[probableBoxes, nms]; binarizedMasks = MapThread[( mask = ConstantArray[0, Dimensions[#1]]; imask = Take[#1, #2[[1, 2]] ;; #2[[2, 2]], #2[[1, 1]] ;; #2[[2, 1]]]; mask[[#2[[1, 2]] ;; #2[[2, 2]], #2[[1, 1]] ;; #2[[2, 1]]]] = imask; Binarize[Image[mask, Interleaving -> False], 0.5]) &, {resampledMasks, nmsBoxes} ]
Out[44]=

Visualize the bounding boxes scaled by their class probabilities:

In[45]:=
{w, h} = ImageDimensions[testImage]; imgSize = 640; max = Max[{w, h}]; scale = max/imgSize; {padx, pady} = imgSize*(1 - {w, h}/max)/2; rectangles = Apply[ Function[ x1 = Clip[Floor[scale*(#1 - #3/2 - padx)], {1, w}]; y1 = Clip[Floor[scale*(imgSize - #2 - #4/2 - pady)], {1, h}]; x2 = Clip[Floor[scale*(#1 + #3/2 - padx)], {1, w}]; y2 = Clip[Floor[scale*(imgSize - #2 + #4/2 - pady)], {1, h}]; Rectangle[{x1, y1}, {x2, y2}] ], res["Boxes"], 2 ]; Graphics[ MapThread[ {EdgeForm[Opacity[Total[#1] + .01]], #2} &, {Max /@ res["ClassProb"], rectangles}], BaseStyle -> {FaceForm[], EdgeForm[{Thin, Black}]} ]
Out[51]=

Visualize all the boxes scaled by the probability that they contain a person:

In[52]:=
idx = Position[labels, "person"][[1, 1]];
In[53]:=
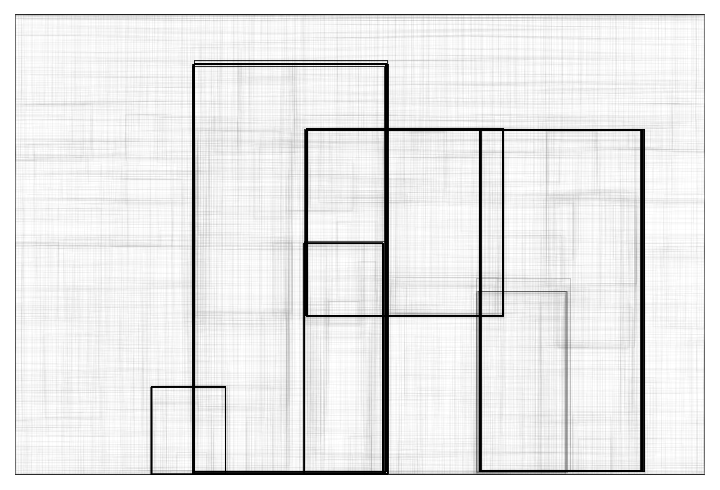
Graphics[ MapThread[{EdgeForm[Opacity[#1 + .01]], #2} &, {Extract[ res["ClassProb"], {All, idx}], rectangles}], BaseStyle -> {FaceForm[], EdgeForm[{Thin, Black}]} ]
Out[53]=

Superimpose the person predictions on top of the input received by the net:

In[54]:=
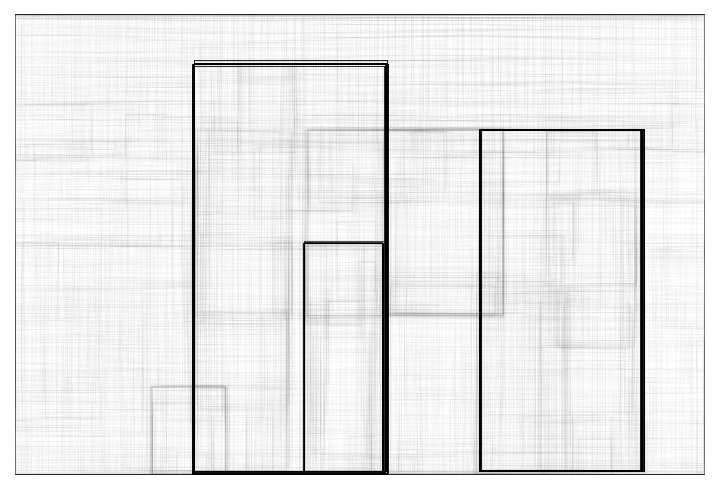
HighlightImage[testImage, Graphics[ MapThread[{EdgeForm[{Thickness[#1/100], Opacity[(#1 + .01)/3]}], #2} &, {Extract[ res["ClassProb"], {All, idx}], rectangles}]], BaseStyle -> {FaceForm[], EdgeForm[{Thin, Red}]}]
Out[54]=

Net information

Inspect the number of parameters of all arrays in the net:

In[55]:=
Information[ NetModel[ "YOLO V8 Segment Trained on MS-COCO Data"], "ArraysElementCounts"]
Out[55]=

Obtain the total number of parameters:

In[56]:=
Information[ NetModel[ "YOLO V8 Segment Trained on MS-COCO Data"], "ArraysTotalElementCount"]
Out[56]=

Obtain the layer type counts:

In[57]:=
Information[ NetModel[ "YOLO V8 Segment Trained on MS-COCO Data"], "LayerTypeCounts"]
Out[57]=

Display the summary graphic:

In[58]:=
Information[ NetModel[ "YOLO V8 Segment Trained on MS-COCO Data"], "SummaryGraphic"]
Out[58]=

Resource History

  • Date Created: 1 September 2023
  • Latest Update: 5 October 2023

Reference