Wolfram Neural Net Repository

Immediate Computable Access to Neural Net Models

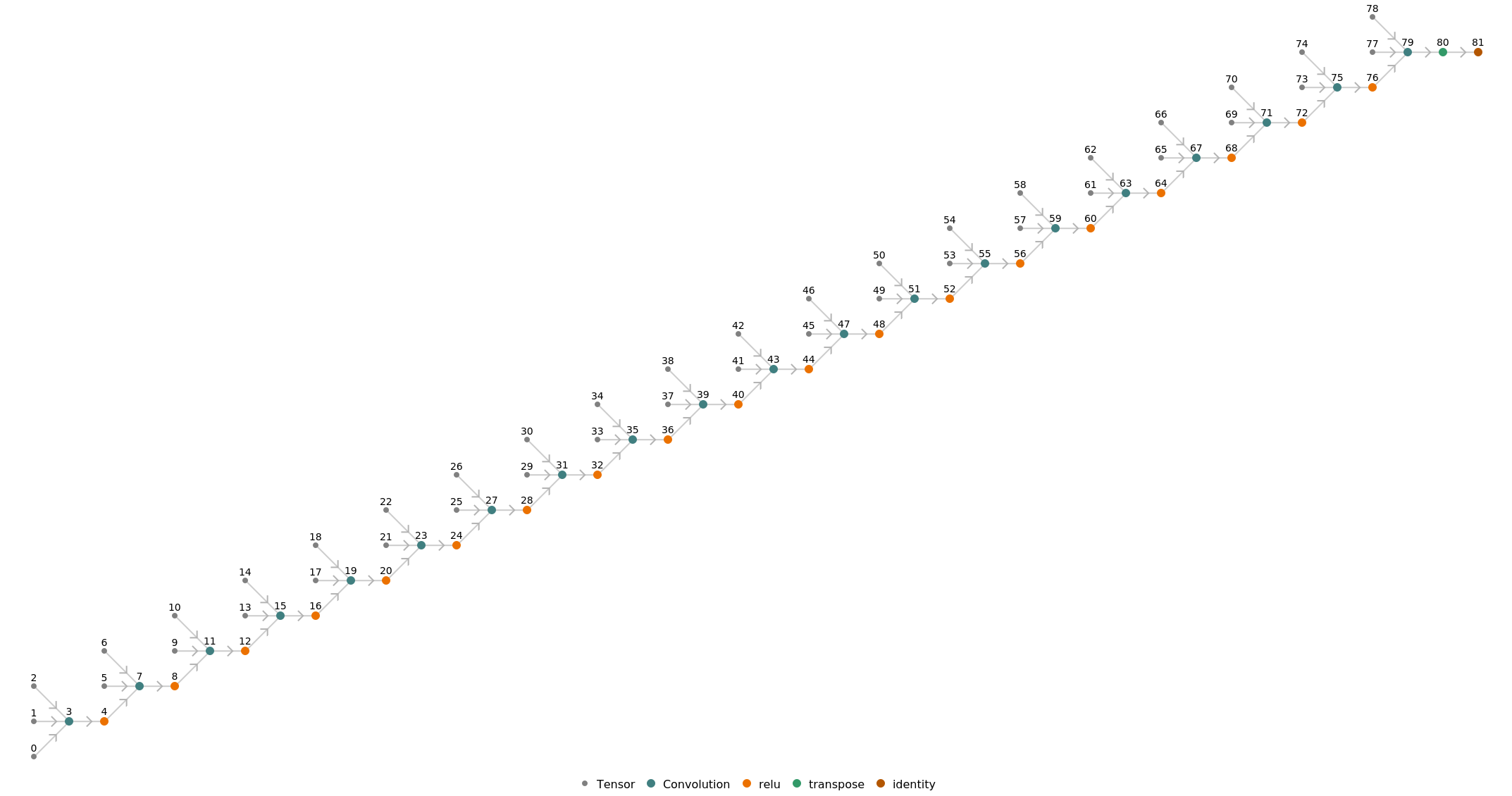
Very Deep Net for Super-Resolution

Increase the resolution of an image

Released in 2016, this net uses an architecture inspired by VGG in order to create super-resolution images. It takes an interpolated low-resolution image and refines the details to create a sharp upsampling.

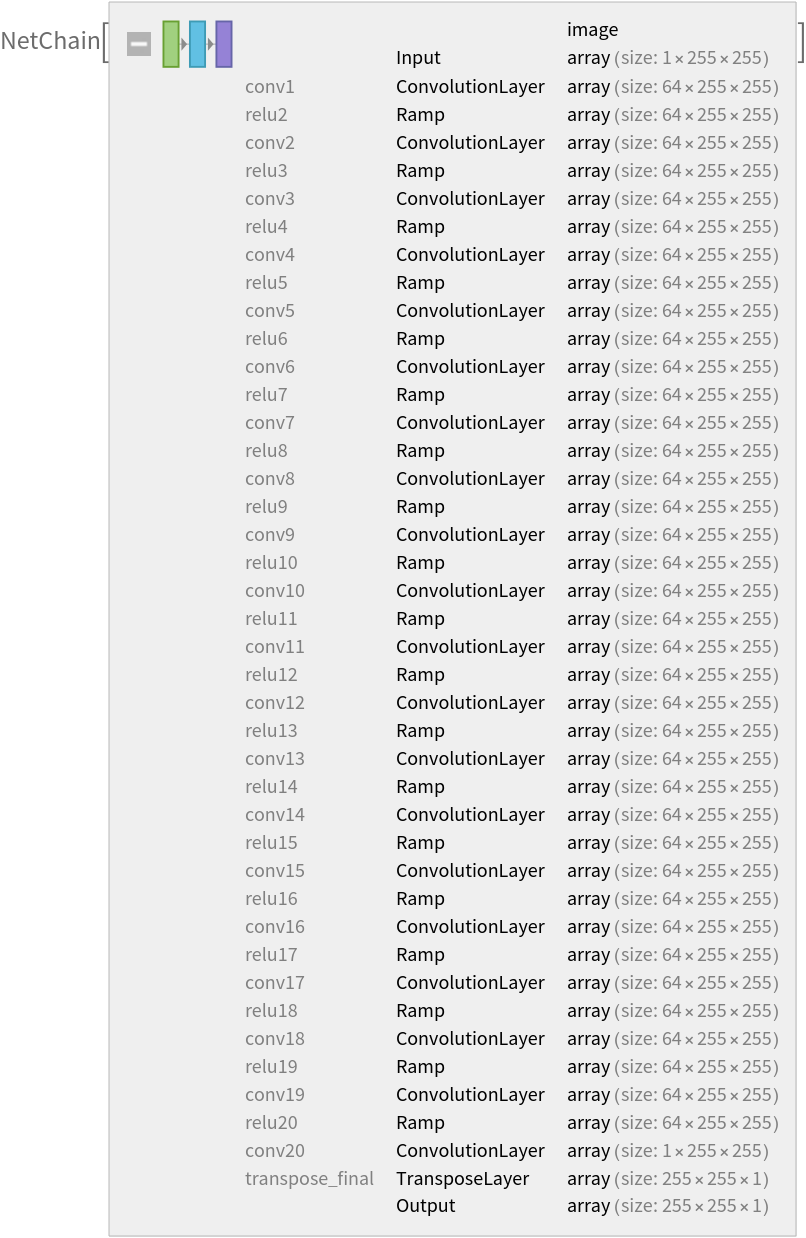
Number of layers: 40 | Parameter count: 665,921 | Trained size: 3 MB |

Training Set Information

Performance

Examples

Resource retrieval

Get the pre-trained net:

In[1]:=
NetModel["Very Deep Net for Super-Resolution"]
Out[1]=

Evaluation function

Write an evaluation function to handle net resizing and color conversion:

In[2]:=
netevaluate[img_, imgScale_] := Block[{net, interpolated, ycbcr, channels, resizedNet, diff, rgb}, net = NetModel["Very Deep Net for Super-Resolution"]; interpolated = ImageResize[img, Scaled[imgScale], Resampling -> "Cubic"];(* upscale to the final size *) ycbcr = ImageApply[{{0.257, 0.504, 0.098}, {-0.148, -0.291, 0.439}, {0.439, -0.368, -0.071}}.# + {0.063, 0.502, 0.502} &, interpolated]; channels = ColorSeparate[ycbcr]; resizedNet = NetReplacePart[net, "Input" -> NetEncoder[{"Image", ImageDimensions@interpolated, ColorSpace -> "Grayscale"}]]; diff = Image@resizedNet[channels[[1]]]; ycbcr = ColorCombine[{channels[[1]] + diff, channels[[2]], channels[[3]]}]; rgb = ImageApply[{{1.164, 0., 1.596}, {1.164, -0.392, -0.813}, {1.164, 2.017, 0.}}.# + {-0.874, 0.532, -1.086} &, ycbcr]; rgb ]

Basic usage

Get an image:

In[3]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/428e8456-38ea-4841-977d-e0422f89dde5"]

Downscale the image by a factor of 3:

In[4]:=
zoom = 3;
In[5]:=
downScaled = ImageResize[img, Scaled[1/zoom]]
Out[5]=

Upscale the downscaled image using the net:

In[6]:=
upScaled = netevaluate[downScaled, zoom]
Out[6]=

Compare the details with a naively upscaled version:

In[7]:=
ImageAssemble@ Table[ImageTrim[ img, {{360, 50}, {430, 200}}], {img, {upScaled, ImageResize[downScaled, Scaled[zoom]]}}]
Out[7]=

Evaluate the peak signal-to-noise ratio:

In[8]:=
10*Log[10, 1/Mean@Flatten@ImageData[(upScaled - img)^2]]
Out[8]=

Net information

Inspect the number of parameters of all arrays in the net:

In[9]:=
NetInformation[ NetModel["Very Deep Net for Super-Resolution"], \ "ArraysElementCounts"]
Out[9]=

Obtain the total number of parameters:

In[10]:=
NetInformation[ NetModel["Very Deep Net for Super-Resolution"], \ "ArraysTotalElementCount"]
Out[10]=

Obtain the layer type counts:

In[11]:=
NetInformation[ NetModel["Very Deep Net for Super-Resolution"], "LayerTypeCounts"]
Out[11]=

Display the summary graphic:

In[12]:=
NetInformation[ NetModel["Very Deep Net for Super-Resolution"], "SummaryGraphic"]
Out[12]=

Export to MXNet

Export the net into a format that can be opened in MXNet:

In[13]:=
jsonPath = Export[FileNameJoin[{$TemporaryDirectory, "net.json"}], NetModel["Very Deep Net for Super-Resolution"], "MXNet"]
Out[13]=

Export also creates a net.params file containing parameters:

In[14]:=
paramPath = FileNameJoin[{DirectoryName[jsonPath], "net.params"}]
Out[14]=

Get the size of the parameter file:

In[15]:=
FileByteCount[paramPath]
Out[15]=

The size is similar to the byte count of the resource object:

In[16]:=
ResourceObject["Very Deep Net for Super-Resolution"]["ByteCount"]
Out[16]=

Represent the MXNet net as a graph:

In[17]:=
Import[jsonPath, {"MXNet", "NodeGraphPlot"}]
Out[17]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Resource History

  • Date Created: 26 July 2018

Reference

  • J. Kim, J. Kwon Lee and K. Mu Lee, "Accurate Image Super-Resolution Using Very Deep Convolutional Networks," Proc. of IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2016)
  • Available from: https://github.com/huangzehao/caffe-vdsr
  • Rights: MIT License