Resource retrieval
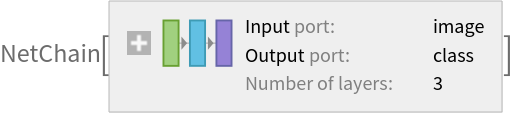
Get the pre-trained net:
Basic usage
Classify an image:
The prediction is an Entity object, which can be queried:
Get a list of available properties of the predicted Entity:
Obtain the probabilities of the ten most likely entities predicted by the net:
An object outside the list of the ImageNet classes will be misidentified:
Obtain the list of names of all available classes:
Feature extraction
Remove the last three layers of the trained net so that the net produces a vector representation of an image:
Get a set of images:
Visualize the features of a set of images:
Visualize convolutional weights
Extract the weights of the first convolutional layer in the trained net:
Visualize the weights as a list of 64 images of size 3x3:
Transfer learning
Use the pre-trained model to build a classifier for telling apart images of dogs and cats. Create a test set and a training set:
Remove the linear layer from the pre-trained net:
Create a new net composed of the pre-trained net followed by a linear layer and a softmax layer:
Train on the dataset, freezing all the weights except for those in the "linearNew" layer (use TargetDevice -> "GPU" for training on a GPU):
Perfect accuracy is obtained on the test set:
Net information
Inspect the number of parameters of all arrays in the net:
Obtain the total number of parameters:
Obtain the layer type counts:
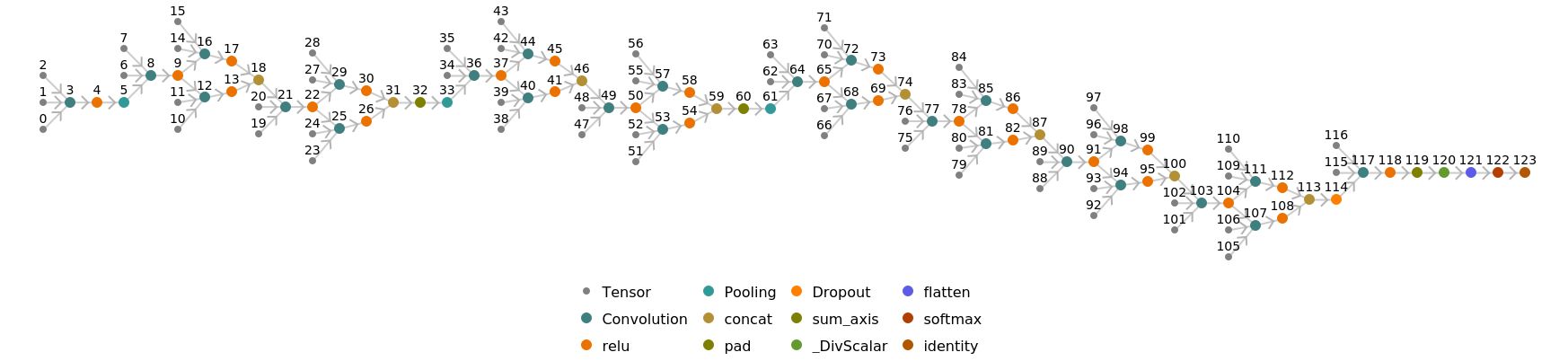
Display the summary graphic:
Export to MXNet
Export the net into a format that can be opened in MXNet:
Export also creates a net.params file containing parameters:
Get the size of the parameter file:
The size is similar to the byte count of the resource object:
Represent the MXNet net as a graph:

![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/0bf855f0-8710-4304-8d76-2557ec82b1f9"]](https://www.wolframcloud.com/obj/resourcesystem/images/ef9/ef989b1b-6021-470b-818f-6d5d41783473/05c1b4ccafe224d7.png)

![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/359b8848-24c1-406f-9844-d27dd612343d"]](https://www.wolframcloud.com/obj/resourcesystem/images/ef9/ef989b1b-6021-470b-818f-6d5d41783473/3f0a8c12ce96f883.png)

![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/9cdd7d89-11da-4db5-99d9-93969e7b1c24"]](https://www.wolframcloud.com/obj/resourcesystem/images/ef9/ef989b1b-6021-470b-818f-6d5d41783473/5b3882dd7b2ea623.png)
![EntityValue[
NetExtract[
NetModel["SqueezeNet V1.1 Trained on ImageNet Competition Data"], "Output"][["Labels"]], "Name"]](https://www.wolframcloud.com/obj/resourcesystem/images/ef9/ef989b1b-6021-470b-818f-6d5d41783473/1e6937a587e28fa4.png)


![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/45b60883-1a11-4e51-abe5-52eece372e7c"]](https://www.wolframcloud.com/obj/resourcesystem/images/ef9/ef989b1b-6021-470b-818f-6d5d41783473/0fe9ee65be58792b.png)


![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/a6cc20ee-d8c4-461e-9b76-7c89800cdbf1"]](https://www.wolframcloud.com/obj/resourcesystem/images/ef9/ef989b1b-6021-470b-818f-6d5d41783473/6b45e8f8d9808849.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/9ee577a4-73db-4383-b3fc-b360c40bd26d"]](https://www.wolframcloud.com/obj/resourcesystem/images/ef9/ef989b1b-6021-470b-818f-6d5d41783473/60362245cee9696f.png)

![newNet = NetChain[<|"pretrainedNet" -> tempNet, "linearNew" -> LinearLayer[], "softmax" -> SoftmaxLayer[]|>, "Output" -> NetDecoder[{"Class", {"cat", "dog"}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/ef9/ef989b1b-6021-470b-818f-6d5d41783473/75df45ac0666d5c3.png)