GPT Transformer Trained on BookCorpus Data

Generate text in English and represent text as a sequence of vectors

Released in 2018, this Generative Pre-Training Transformer (GPT) model is pre-trained in an unsupervised fashion on a large corpus of English text. This model can be further fine-tuned with additional output layers to create highly accurate NLP models for a wide range of tasks. It uses bi-directional causal self-attention, often referred to as a transformer decoder.

Number of models: 2

Training Set Information

BookCorpus, a dataset consisting of 11,038 unpublished books from 16 different genres.

Performance

The model fine-tuned on various datasets obtains the following accuracy on various natural language inference tasks: 82.1%, 81.4%, 89.9%, 88.3%, 88.1% and 56% accuracy on MNLI-m, MNLI-mm, SNLI, SciTail, QNLI, and RTE datasets respectively.

For question answering and commonsense reasoning, the fine-tuned model obtains the following accuracies: 86.5%, 62.9%, 57.4%, and 59.0% accuracy on Story Cloze, RACE-m, RACE-h, and RACE datasets respectively

Examples

Download Example Notebook

Open in Wolfram Cloud

Resource retrieval

Get the pre-trained net:

In[1]:=

Out[1]=

NetModel parameters

This model consists of a family of individual nets, each identified by a specific parameter combination. Inspect the available parameters:

In[2]:=

$NetModel["GPT Transformer Trained on BookCorpus Data", \ "ParametersInformation"]$

Out[2]=

Pick a non-default net by specifying the parameters:

In[3]:=

Out[3]=

Pick a non-default uninitialized net:

In[4]:=

Out[4]=

Basic usage

Given a piece of text, the GPT net produces a sequence of feature vectors of size 768, which correspond to the sequence of input words or subwords:

In[5]:=

Out[5]=

Obtain dimensions of the embeddings:

In[6]:=

Out[6]=

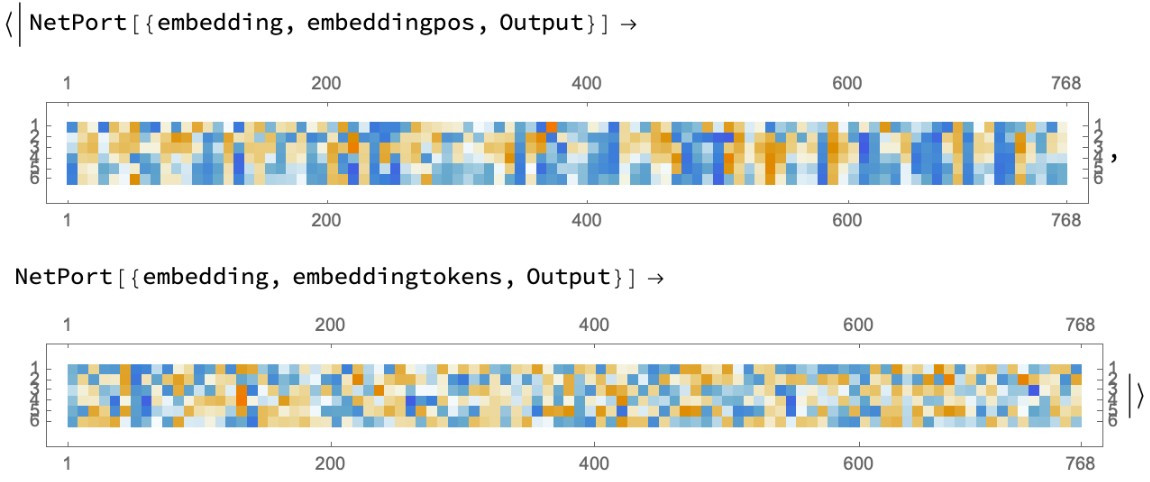
Visualize the embeddings:

In[7]:=

Out[7]=

Transformer architecture

The input string is first normalized and then tokenized, or split into words or subwords. This two-step process is accomplished using the NetEncoder "Function":

In[8]:=

Out[9]=

The tokenization step is performed using the NetEncoder "BPESubwordTokens" and can be extracted using the following steps:

In[10]:=

The encoder produces an integer index for each subword token that corresponds to the position in the vocabulary:

In[11]:=

Out[11]=

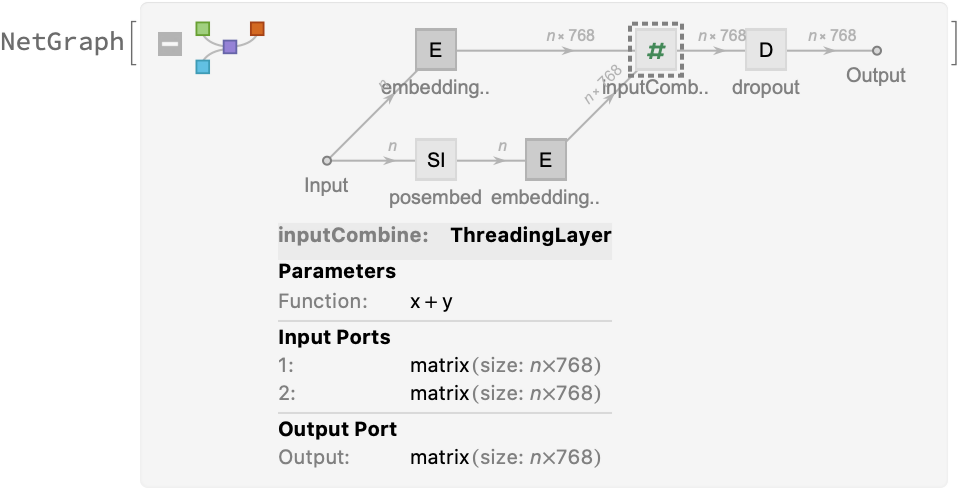
Each subword token is also assigned a positional index:

In[12]:=

Out[12]=

A lookup is done to map these indices to numeric vectors of size 768:

In[13]:=

embeddings = net["Hello world! I am here", {NetPort[{"embedding", "embeddingpos",
"Output"}], NetPort[{"embedding", "embeddingtokens", "Output"}]}];
Map[MatrixPlot, embeddings]

Out[14]=

For each subword token, these two embeddings are combined by summing elements with ThreadingLayer:

In[15]:=

Out[15]=

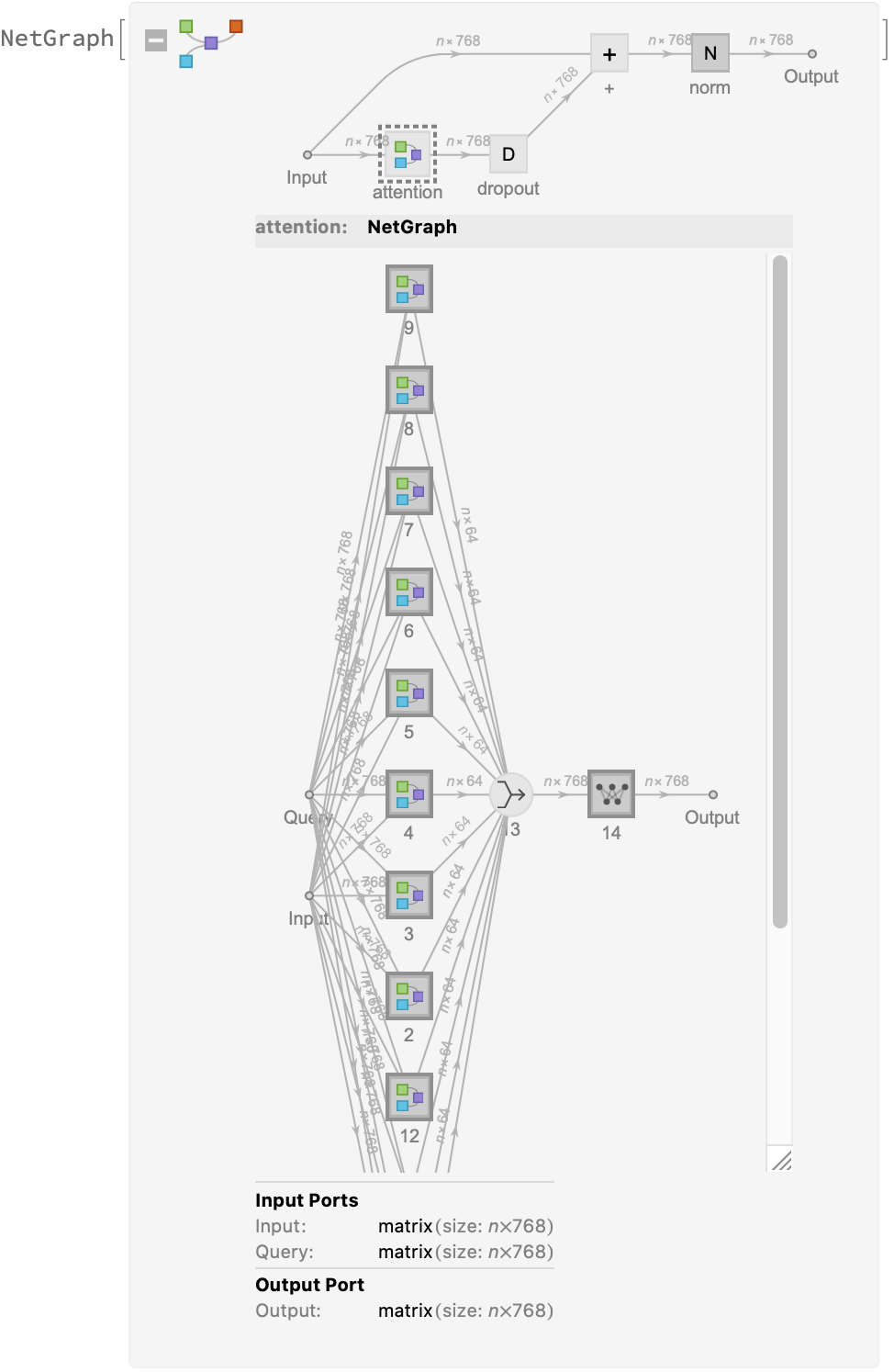
The transformer architecture then processes the vectors using 12 structurally identical self-attention blocks stacked in a chain:

In[16]:=

Out[16]=

The key part of these blocks is the attention module consisting of 12 parallel self-attention transformations, also called “attention heads”:

In[17]:=

Out[17]=

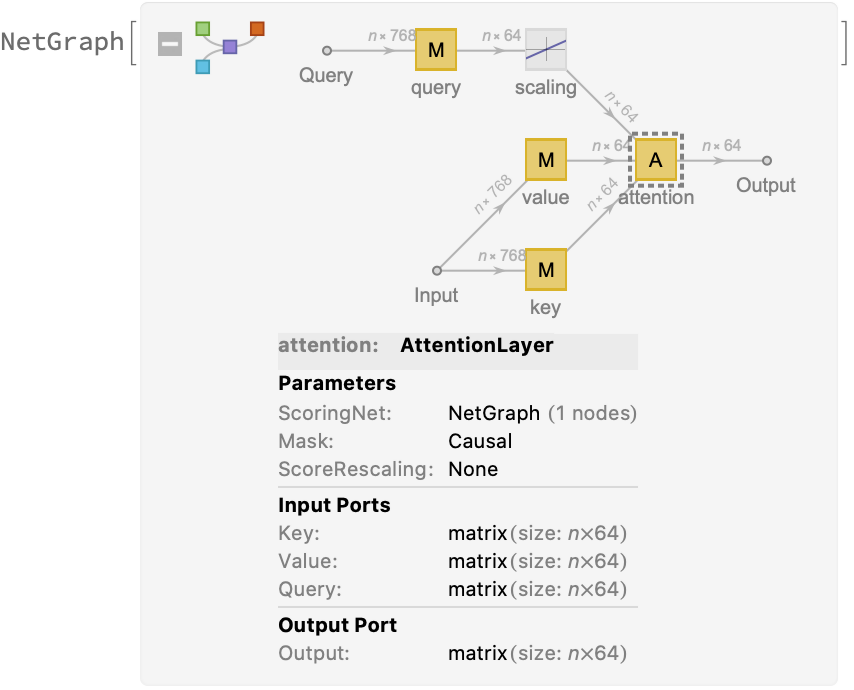
Each head uses an AttentionLayer at its core:

In[18]:=

Out[18]=

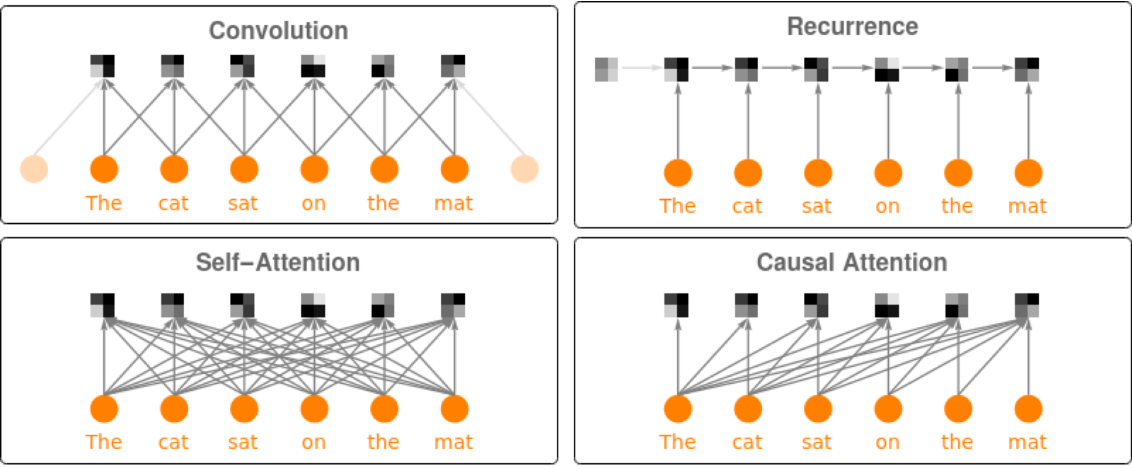
Attention is done with causal masking, which means that the embedding of a given subword token depends on the previous subword tokens and not on the subsequent ones. This is a prerequisite to be able to generate text with the language model. The following figures compare causal attention to other forms of connectivity between input tokens:

Language modeling: Basic usage

Retrieve the language model by specifying the "Task" parameter:

In[19]:=

Out[19]=

Predict the next word in a given sequence:

In[20]:=

Out[20]=

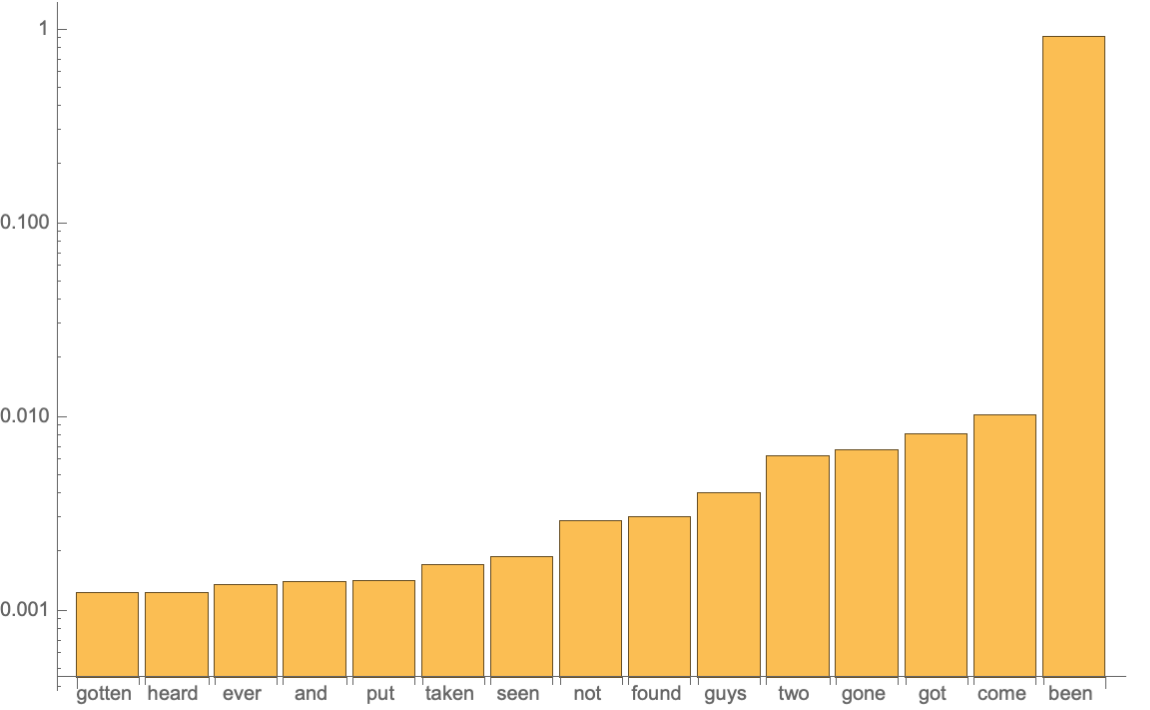
Obtain the top 15 probabilities:

In[21]:=

Out[21]=

Plot the top 15 probabilities:

In[22]:=

$BarChart[Thread@ Labeled[Values@topProbs, Keys[topProbs] /. {"\n" -> "\\n", "\t" -> "\\t"}], ScalingFunctions -> "Log", ImageSize -> Large]$

Out[22]=

Text generation

Modify the language model so that it accepts the encoded token indices as input and creates the token indices as output:

In[23]:=

lm = NetModel[{"GPT Transformer Trained on BookCorpus Data", "Task" -> "LanguageModeling"}];
encoder = NetExtract[lm, "Input"];
netdecoder = NetExtract[lm, "Output"];
numwords = NetExtract[netdecoder, "Dimensions"];
languagemodel = NetReplacePart[lm,
{"Input" -> None,
"Output" -> NetDecoder[{"Class", Range@numwords}]}];

Create a new decoder that performs a lookup to find the corresponding string, followed by some text cleaning:

In[24]:=

$assoc = AssociationThread[ Range@numwords -> NetExtract[netdecoder, "Labels"]]; decoder = Function[array, StringReplace[ StringJoin@Lookup[assoc, array], {"\n " -> "\n", " " ~~ x : PunctuationCharacter :> x}]];$

Define a function to predict the next token using the modified language model:

In[25]:=

$generateSample[{lmmodified_, encoder_, decoder_}][input_String, numTokens_ : 10, temperature_ : 1] := Module[{numwords, inputcodes, outputcodes, matrix}, inputcodes = encoder[input]; outputcodes = Nest[Function[ Join[#, {lmmodified[#, {"RandomSample", "Temperature" -> temperature}]}]], inputcodes, numTokens]; decoder[outputcodes]]$

Get an input:

In[26]:=

Out[26]=

Generate the next 20 tokens by using it on the input:

In[27]:=

Out[27]=

The third optional argument is a “temperature” parameter that scales the input to the final softmax. A high temperature flattens the distribution from which tokens are sampled, increasing the probability of extracting less likely tokens:

In[28]:=

Out[28]=

Decreasing the temperature sharpens the peaks of the sampling distribution, further decreasing the probability of extracting less likely tokens:

In[29]:=

Out[29]=

Very high temperature settings are equivalent to random sampling:

In[30]:=

Out[30]=

Very low temperature settings are equivalent to always picking the character with maximum probability. It is typical for sampling to “get stuck in a loop”:

In[31]:=

Out[31]=

Sentence analogies

Define a sentence embedding that consists of the last subword embedding of GPT (this choice is justified by the fact that GPT is a forward causal model):

In[32]:=

Out[32]=

Define some sentences in two broad categories for comparison:

In[33]:=

sentences = {"I put on some nice soothing music.", "The song blasted from the little radio.", "The soundtrack from the movie was so good.", "Food is needed for survival.", "Go on, eat if you are hungry.", "Her baking skills are terrible."};

Precompute the embeddings for a list of sentences:

In[34]:=

Visualize the similarity between the sentences using the net as a feature extractor:

In[35]:=

Out[35]=

Train a classifier with the subword embeddings

Get a text-processing dataset:

In[36]:=

View a random sample of the dataset:

In[37]:=

Out[37]=

Define a sentence embedding that consists of the last subword embedding of GPT (this choice is justified by the fact that GPT is a forward causal model):

In[38]:=

Out[38]=

Precompute the GPT vectors for the training and the validation datasets (if available, GPU is highly recommended):

In[39]:=

Define a simple network for classification:

In[40]:=

Out[41]=

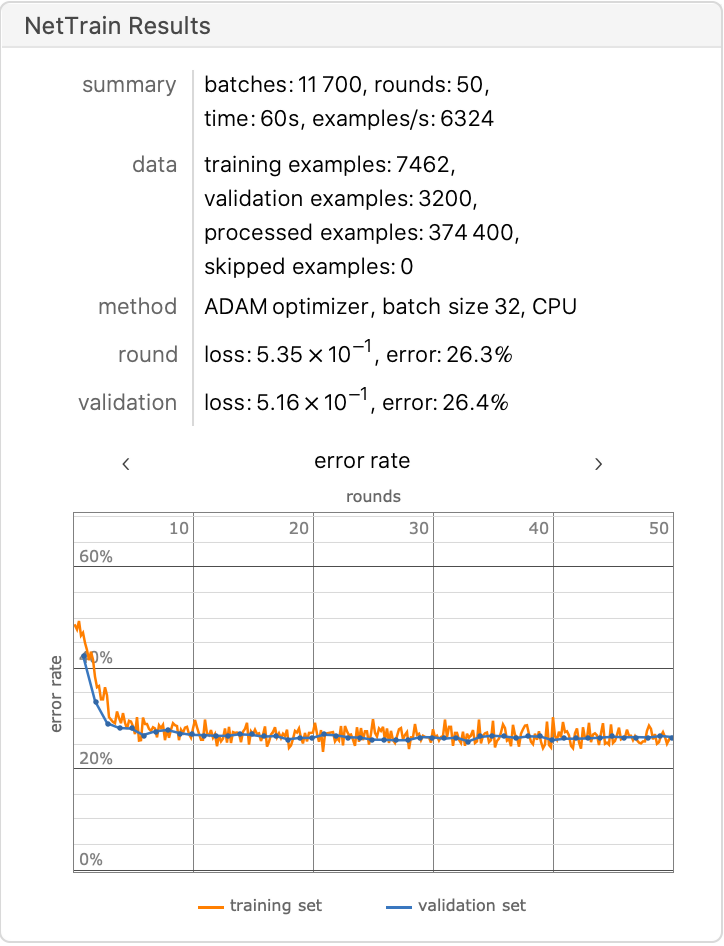
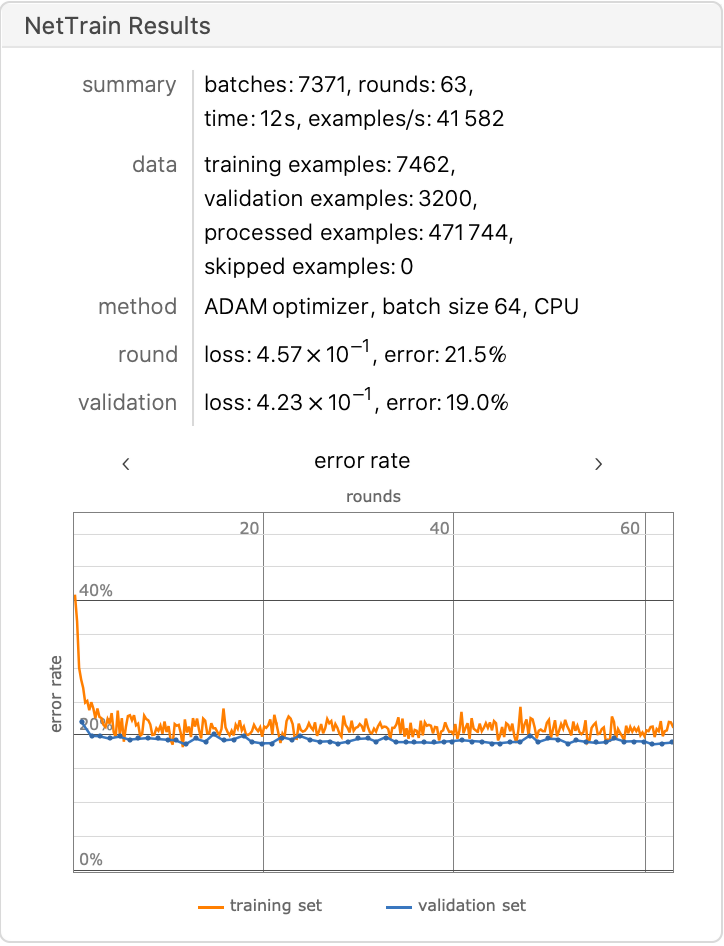
Train the network on the precomputed GPT vectors:

In[42]:=

gptresults = NetTrain[classifierhead, trainembeddings, All,
ValidationSet -> validembeddings,
TrainingStoppingCriterion -> <|"Criterion" -> "ErrorRate", "Patience" -> 50|>,
TargetDevice -> "CPU",
MaxTrainingRounds -> 500]

Out[42]=

Check the classification error rate on the validation data:

In[43]:=

Out[43]=

Compare the results with the performance of a classifier trained on context-independent word embeddings. Precompute the GloVe vectors for the training and the validation datasets (if available, GPU is recommended):

In[44]:=

$glove = NetModel[ "GloVe 300-Dimensional Word Vectors Trained on Wikipedia and \ Gigaword 5 Data"];$

In[45]:=

Define a simple network for classification, using a max-pooling strategy:

In[46]:=

gloveclassifierhead = NetChain[
{DropoutLayer[],
NetMapOperator[2],
AggregationLayer[Max, 1],
SoftmaxLayer[]},
"Output" -> NetDecoder[{"Class", {"negative", "positive"}}]]

Out[46]=

Train the classifier on the precomputed GloVe vectors:

In[47]:=

gloveresults = NetTrain[gloveclassifierhead, trainembeddingsglove, All,
ValidationSet -> validembeddingsglove,
TrainingStoppingCriterion -> <|"Criterion" -> "ErrorRate", "Patience" -> 50|>,
TargetDevice -> "CPU",
MaxTrainingRounds -> 50]

Out[47]=

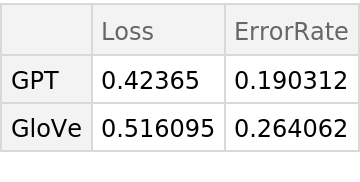
Compare the results obtained with GPT and with GloVe:

In[48]:=

Out[48]=

Net information

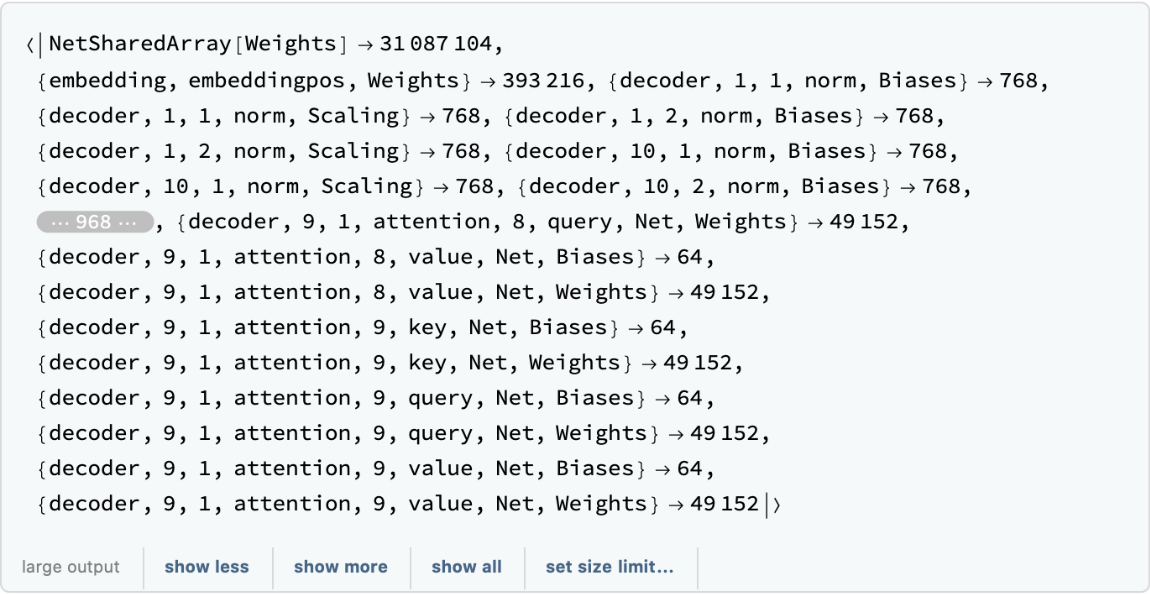
Inspect the number of parameters of all arrays in the net:

In[49]:=

$NetInformation[ NetModel["GPT Transformer Trained on BookCorpus Data"], \ "ArraysElementCounts"]$

Out[49]=

Obtain the total number of parameters:

In[50]:=

$NetInformation[ NetModel["GPT Transformer Trained on BookCorpus Data"], \ "ArraysTotalElementCount"]$

Out[50]=

Obtain the layer type counts:

In[51]:=

$NetInformation[ NetModel["GPT Transformer Trained on BookCorpus Data"], \ "LayerTypeCounts"]$

Out[51]=

Display the summary graphic:

In[52]:=

$NetInformation[ NetModel["GPT Transformer Trained on BookCorpus Data"], \ "SummaryGraphic"]$

Out[52]=

Export to MXNet

Export the net into a format that can be opened in MXNet:

In[53]:=

Out[53]=

Export also creates a net.params file containing parameters:

In[54]:=

Out[54]=

Get the size of the parameter file:

In[55]:=

Out[55]=

Construction Notebook

Download Construction Notebook

Open in Wolfram Cloud

Requirements

Wolfram Language 12.0 (April 2019) or above

External Links

https://s3-us-west-2.amazonaws.com/openai-assets/research-covers/language-unsupervised/language_understanding_paper.pdf

Resource History

Date Created: 8 April 2019
Latest Update: 12 April 2019

Reference

A. Radford, K. Narasimhan, T. Salimans, I. Sutskever, "Improving language understanding by generative pre-training," preprint (2018)
Available from: https://github.com/openai/finetune-transformer-lm
Rights: MIT License