EfficientDet
Trained on
MS-COCO Data
Released in 2020, this family of object detection models is obtained by uniformly scaling the resolution, depth, and width of the original EfficientNet models, obtaining larger nets. In addition, a novel weighted bidirectional feature pyramid network (BiFPN) is introduced for fast and easy multiscale feature fusion. EfficientDet-D7 achieves stateof-the-art 55.1 AP on COCO test-dev, being 4x – 9x smaller and using 13x – 42x fewer FLOPs than previous detectors.
Number of models: 9
Examples
Resource retrieval
Get the pre-trained net:
NetModel parameters
This model consists of a family of individual nets, each identified by a specific parameter combination. Inspect the available parameters:
Pick a non-default net by specifying the parameters:
Pick a non-default uninitialized net:
Evaluation function
Write an evaluation function to scale the result to the input image size and suppress the least probable detections:
Basic usage
Obtain the detected bounding boxes with their corresponding classes and confidences for a given image:
Inspect which classes are detected:
Visualize the detection:
Network result
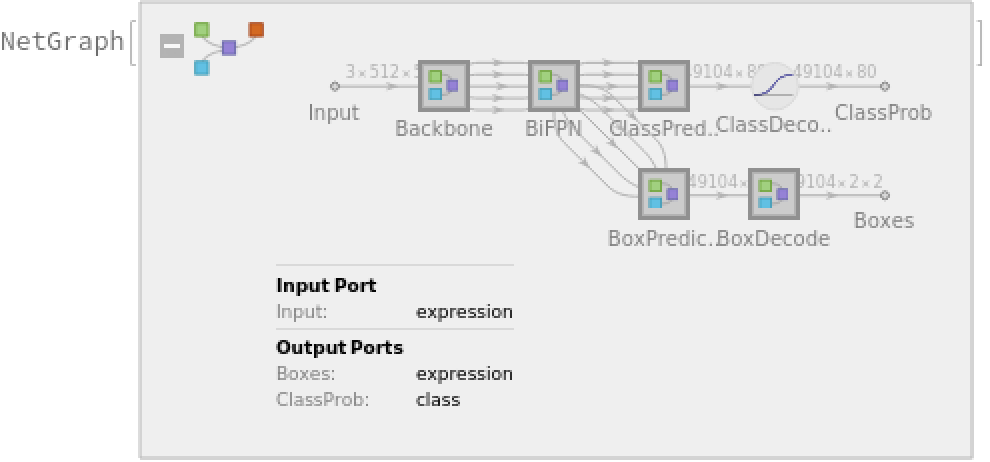
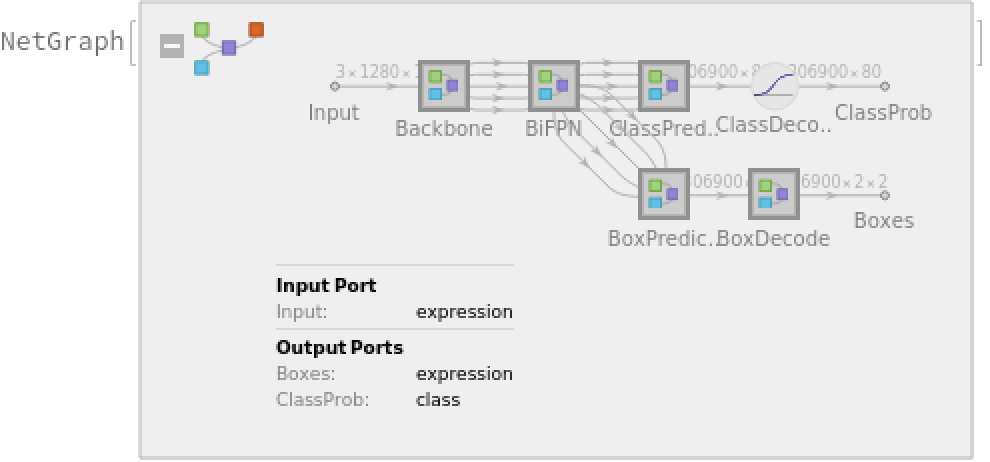
The network computes 49,104 bounding boxes and the probability that the objects in each box are of any given class:
Visualize all the boxes predicted by the net scaled by their "objectness" measures:
Visualize all the boxes scaled by the probability that they contain a cat:
Superimpose the cat prediction on top of the scaled input received by the net:
Net information
Inspect the number of parameters of all arrays in the net:
Obtain the total number of parameters:
Obtain the layer type counts:
Display the summary graphic:
Resource History
Reference



![netevaluate[model_, img_Image, detectionThreshold_ : .5, overlapThreshold_ : .45] := Module[
{netoutput, class2box, argMaxPerBox, maxPerBox, maxClasses, probableDetectionInd, probableClasses, probableScores, probableBoxes, nmsDetections, boxDecoder, scale, targetSize},
netoutput = model[img, {"ClassProb" -> "Probabilities", "Boxes"}];
class2box = Transpose@Values[netoutput["ClassProb"]];
(*Assuming there is one class per box*) argMaxPerBox = Flatten@Map[ Ordering[#, -1] &, class2box];
maxPerBox = Map[Max, class2box];
maxClasses = Keys[netoutput["ClassProb"]][[argMaxPerBox]];
(*Filter out the low score boxes*) probableDetectionInd = UnitStep[maxPerBox - detectionThreshold]; probableClasses = Pick[maxClasses, probableDetectionInd, 1];
probableScores = Pick[maxPerBox, probableDetectionInd, 1];
probableBoxes = Pick[netoutput["Boxes"], probableDetectionInd, 1];
(*Apply NMS*) nmsDetections = nonMaximumSuppression[
probableBoxes -> probableScores, {"Region", "Index"}, MaxOverlapFraction -> overlapThreshold]; targetSize = Reverse@Rest[NetExtract[model, {"Input", "Output"}]]; scale = Max[ImageDimensions[img]/targetSize]; boxDecoder[{{a_, b_}, {c_, d_}}, {w_, h_}] := Rectangle[{a*scale, h - b*scale}, {c*scale, h - d*scale}]; Map[{boxDecoder[ First[#], ImageDimensions[img]], probableClasses[[Last[#]]], probableScores[[Last[#]]]} &, nmsDetections]
]](https://www.wolframcloud.com/obj/resourcesystem/images/b67/b6708679-ac82-490d-87bb-5761a465988c/23a4f9e73773172c.png)

![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/239d530e-6e7a-419f-8ded-d663123f0682"]](https://www.wolframcloud.com/obj/resourcesystem/images/b67/b6708679-ac82-490d-87bb-5761a465988c/23995765bd345ffe.png)

![Graphics[
MapThread[{EdgeForm[Opacity[Total[#1] + .01]], #2} &, {probabilities,
rectangles}],
BaseStyle -> {FaceForm[], EdgeForm[{Thin, Black}]}
]](https://www.wolframcloud.com/obj/resourcesystem/images/b67/b6708679-ac82-490d-87bb-5761a465988c/6e892937d73f223e.png)

![Graphics[
MapThread[{EdgeForm[Opacity[#1 + .01]], #2} &, {probabilities[[All, idx]], rectangles}],
BaseStyle -> {FaceForm[], EdgeForm[{Thin, Black}]}
]](https://www.wolframcloud.com/obj/resourcesystem/images/b67/b6708679-ac82-490d-87bb-5761a465988c/4dbb001e74031a44.png)

![HighlightImage[ImageResize[testImage, {512}], Graphics[MapThread[{EdgeForm[{Opacity[#1 + .01]}], #2} &, {probabilities[[All, idx]], rectangles}]], BaseStyle -> {FaceForm[], EdgeForm[{Thin, Red}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/b67/b6708679-ac82-490d-87bb-5761a465988c/0afa9c9c985e027c.png)



![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/5baef553-41a6-4ac6-8925-0eed11ff86ea"]](https://www.wolframcloud.com/obj/resourcesystem/images/b67/b6708679-ac82-490d-87bb-5761a465988c/4aed9f854a0df590.png)