Resource retrieval
Get the pre-trained net:
| Out[1]= |  |
NetModel parameters
This model consists of a family of individual nets, each identified by a specific parameter combination. Inspect the available parameters:
| Out[2]= |  |
Pick a non-default net by specifying the parameters:
| Out[3]= |  |
Pick a non-default uninitialized net:
| Out[4]= |  |
Basic usage
Given a piece of text, the BERT net produces a sequence of feature vectors of size 768, which correspond to the sequence of input words or subwords:
Obtain dimensions of the embeddings:
| Out[6]= | 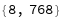 |
Visualize the embeddings:
| Out[7]= |  |
Transformer architecture
Each input text segment is first tokenized into words or subwords using a word-piece tokenizer and additional text normalization. Integer codes called token indices are generated from these tokens, together with additional segment indices:
| Out[9]= |  |
For each input subword token, the encoder yields a pair of indices that correspond to the token index in the vocabulary, and the index of the sentence within the list of input sentences:
| Out[10]= | 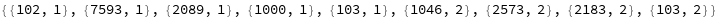 |
The list of tokens always starts with special token index 102, which corresponds to the classification index.
Also the special token index 103 is used as a separator between the different text segments. Each subword token is also assigned a positional index:
| Out[11]= |  |
A lookup is done to map these indices to numeric vectors of size 768:
| Out[13]= | 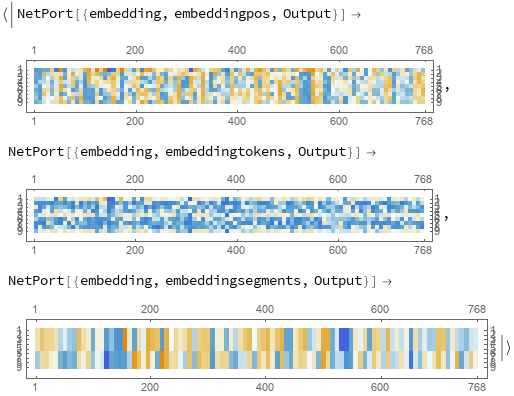 |
For each subword token, these three embeddings are combined by summing elements with ThreadingLayer:
| Out[14]= | 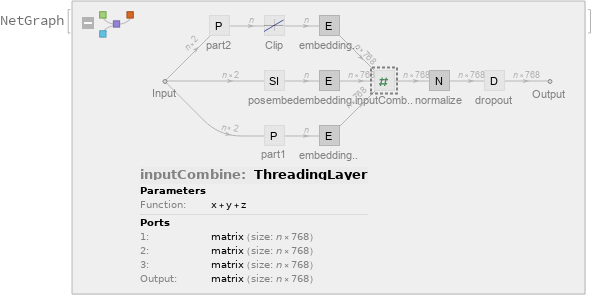 |
The transformer architecture then processes the vectors using 12 structurally identical self-attention blocks stacked in a chain:
| Out[15]= |  |
The key part of these blocks is the attention module comprising of 12 parallel self-attention transformations, also called “attention heads”:
| Out[16]= | 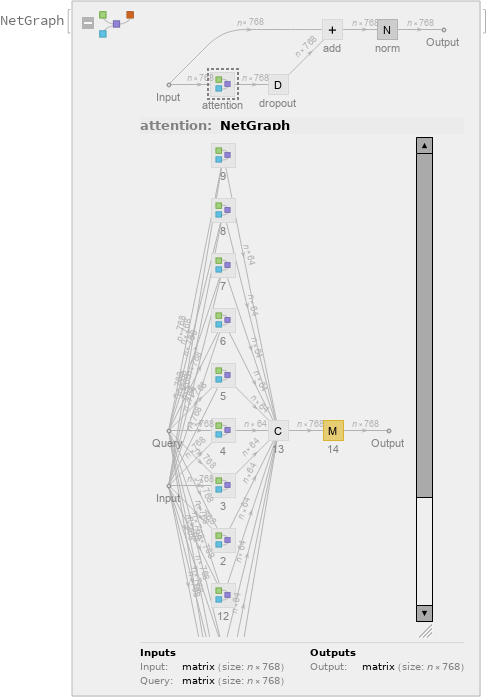 |
Each head uses an AttentionLayer at its core:
| Out[17]= | 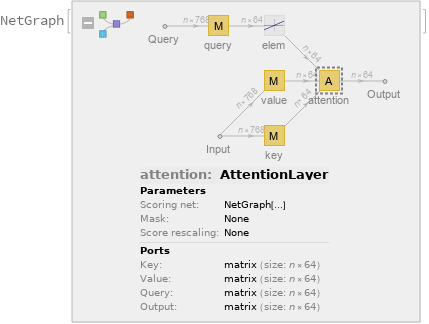 |
BERT uses self-attention, where the embedding of a given subword depends on the full input text. The following figure compares self-attention (lower left) to other types of connectivity patterns that are popular in deep learning:
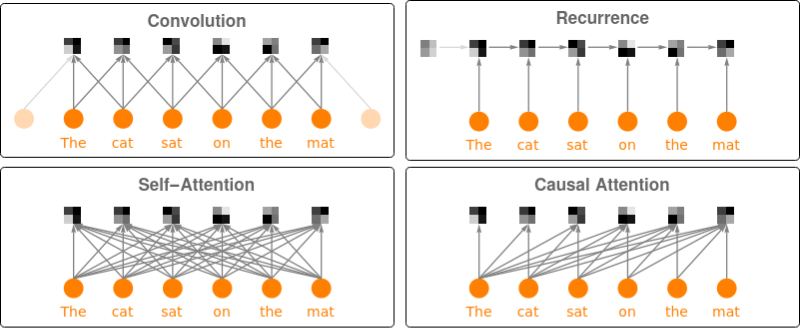
Sentence analogies
Define a sentence embedding that takes the last feature vector from BERT subword embeddings (as an arbitrary choice):
| Out[18]= |  |
Define a list of sentence in two broad categories (food and music):
Precompute the embeddings for a list of sentences:
Visualize the similarity between the sentences using the net as a feature extractor:
| Out[21]= |  |
Train a classifier model with the subword embeddings
Get a text-processing dataset:
View a random sample of the dataset:
| Out[23]= |  |
Precompute the BERT vectors for the training and the validation datasets (if available, GPU is highly recommended):
Define a network to classify the sequences of subword embeddings, using a max-pooling strategy:
| Out[25]= |  |
Train the network on the precomputed BERT vectors:
| Out[26]= | 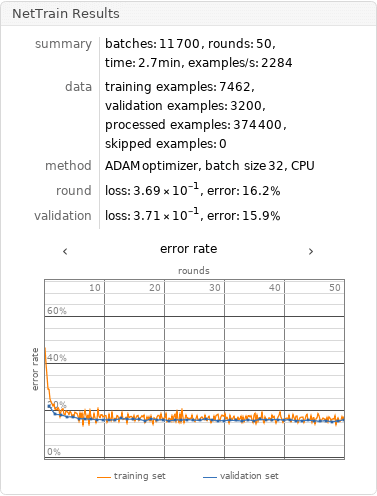 |
Check the classification error rate on the validation data:
| Out[27]= | 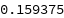 |
Let’s compare the results with the performance of a classifier trained on context-independent word embeddings. Precompute the GloVe vectors for the training and the validation dataset:
Train the classifier on the precomputed GloVe vectors:
| Out[29]= | 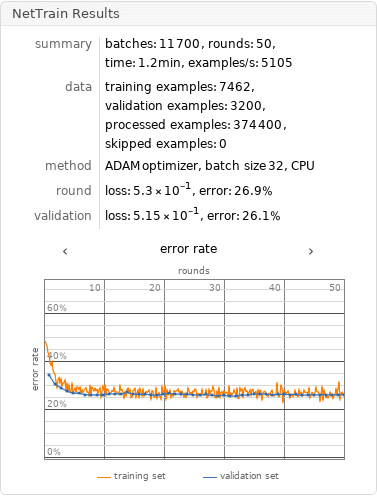 |
Compare the results obtained with GPT and with GloVe:
| Out[30]= | 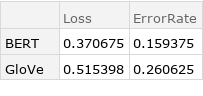 |
Net information
Inspect the number of parameters of all arrays in the net:
| Out[31]= | 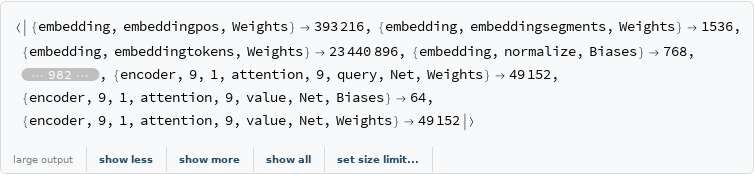 |
Obtain the total number of parameters:
| Out[32]= | 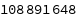 |
Obtain the layer type counts:
| Out[33]= |  |
Display the summary graphic:
| Out[34]= | 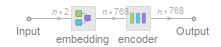 |
Export to MXNet
Export the net into a format that can be opened in MXNet:
| Out[35]= |  |
Export also creates a net.params file containing parameters:
| Out[36]= | 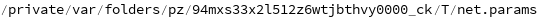 |
Get the size of the parameter file:
| Out[37]= | 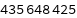 |





![net = NetModel[{"BERT Trained on BookCorpus and English Wikipedia \
Data", "InputType" -> "ListOfStrings"}];
netencoder = NetExtract[net, "Input"]](images/b51/b514b48c-51a3-468b-92f8-357c42e9e825-io-8-i.en.gif)

![embeddings = net[{"Hello world!", "I am here"},
{NetPort[{"embedding", "embeddingpos", "Output"}],
NetPort[{"embedding", "embeddingtokens", "Output"}],
NetPort[{"embedding", "embeddingsegments", "Output"}]}];
Map[MatrixPlot, embeddings]](images/b51/b514b48c-51a3-468b-92f8-357c42e9e825-io-12-i.en.gif)










![trainembeddings =
NetModel["BERT Trained on BookCorpus and English Wikipedia Data"][
train[[All, 1]], TargetDevice -> "CPU"] -> train[[All, 2]];
validembeddings =
NetModel["BERT Trained on BookCorpus and English Wikipedia Data"][
valid[[All, 1]], TargetDevice -> "CPU"] -> valid[[All, 2]];](images/b51/b514b48c-51a3-468b-92f8-357c42e9e825-io-24-i.en.gif)
![classifierhead =
NetChain[{DropoutLayer[], NetMapOperator[2],
AggregationLayer[Max, 1], SoftmaxLayer[]},
"Output" -> NetDecoder[{"Class", {"negative", "positive"}}]]](images/b51/b514b48c-51a3-468b-92f8-357c42e9e825-io-25-i.en.gif)

![bertresults = NetTrain[classifierhead, trainembeddings, All,
ValidationSet -> validembeddings,
TargetDevice -> "CPU",
MaxTrainingRounds -> 50]](images/b51/b514b48c-51a3-468b-92f8-357c42e9e825-io-26-i.en.gif)

![trainembeddingsglove =
NetModel["GloVe 300-Dimensional Word Vectors Trained on Wikipedia \
and Gigaword 5 Data"][train[[All, 1]], TargetDevice -> "CPU"] ->
train[[All, 2]];
validembeddingsglove =
NetModel["GloVe 300-Dimensional Word Vectors Trained on Wikipedia \
and Gigaword 5 Data"][valid[[All, 1]], TargetDevice -> "CPU"] ->
valid[[All, 2]];](images/b51/b514b48c-51a3-468b-92f8-357c42e9e825-io-28-i.en.gif)
![gloveresults = NetTrain[classifierhead, trainembeddingsglove, All,
ValidationSet -> validembeddingsglove,
TrainingStoppingCriterion -> <|"Criterion" -> "ErrorRate",
"Patience" -> 50|>,
TargetDevice -> "CPU",
MaxTrainingRounds -> 50]](images/b51/b514b48c-51a3-468b-92f8-357c42e9e825-io-29-i.en.gif)



