Wolfram Neural Net Repository

Immediate Computable Access to Neural Net Models

GloVe 100-Dimensional Word Vectors Trained on Wikipedia and Gigaword 5 Data

Represent words as vectors

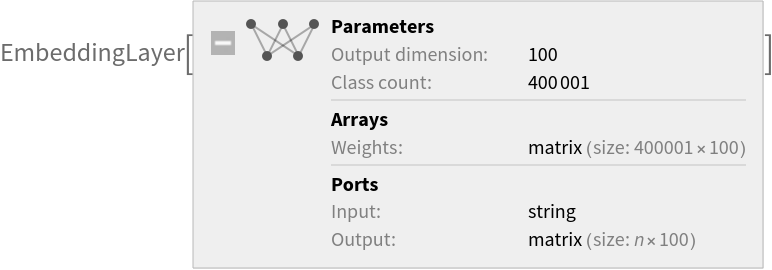
Released in 2014 by the computer science department at Stanford University, this representation is trained using an original method called Global Vectors (GloVe). It encodes 400,000 tokens as unique vectors, with all tokens outside the vocabulary encoded as the zero-vector. Token case is ignored.

Number of layers: 1 | Parameter count: 40,000,100 | Trained size: 163 MB |

Training Set Information

Examples

Resource retrieval

Get the pre-trained net:

In[1]:=
NetModel["GloVe 100-Dimensional Word Vectors Trained on Wikipedia and \ Gigaword 5 Data"]
Out[1]=

Basic usage

Use the net to obtain a list of word vectors:

In[2]:=
vectors = NetModel["GloVe 100-Dimensional Word Vectors Trained on Wikipedia \ and Gigaword 5 Data"]["hello world"]
Out[2]=

Obtain the dimensions of the vectors:

In[3]:=
Dimensions[vectors]
Out[3]=

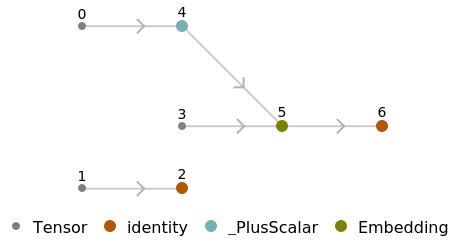
Use the embedding layer inside a NetChain:

In[4]:=
chain = NetChain[{NetModel[ "GloVe 100-Dimensional Word Vectors Trained on Wikipedia and \ Gigaword 5 Data"], LongShortTermMemoryLayer[10]}]
Out[4]=

Feature visualization

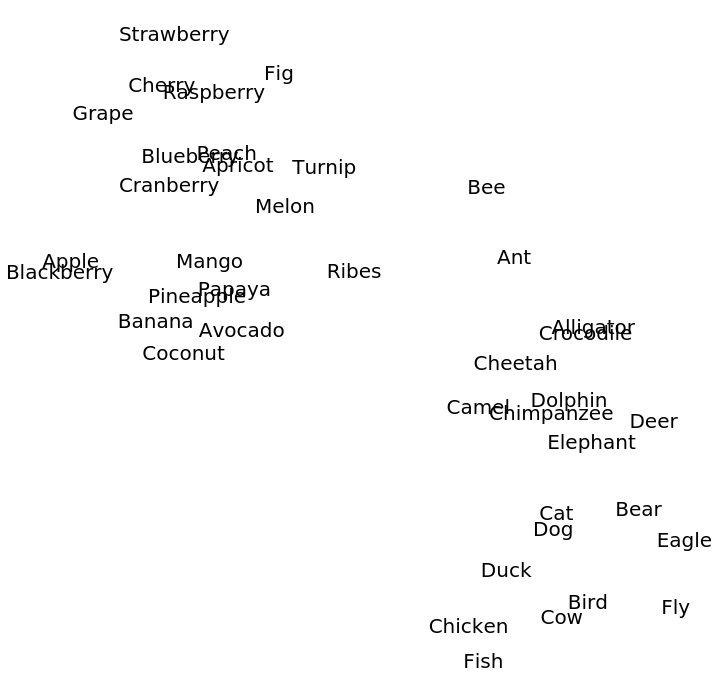
Create two lists of related words:

In[5]:=
animals = {"Alligator", "Ant", "Bear", "Bee", "Bird", "Camel", "Cat", "Cheetah", "Chicken", "Chimpanzee", "Cow", "Crocodile", "Deer", "Dog", "Dolphin", "Duck", "Eagle", "Elephant", "Fish", "Fly"};
In[6]:=
fruits = {"Apple", "Apricot", "Avocado", "Banana", "Blackberry", "Blueberry", "Cherry", "Coconut", "Cranberry", "Grape", "Turnip", "Mango", "Melon", "Papaya", "Peach", "Pineapple", "Raspberry", "Strawberry", "Ribes", "Fig"};

Visualize relationships between the words using the net as a feature extractor:

In[7]:=
FeatureSpacePlot[Join[animals, fruits], FeatureExtractor -> NetModel["GloVe 100-Dimensional Word Vectors Trained on Wikipedia \ and Gigaword 5 Data"]]
Out[7]=

Word analogies

Get the pre-trained net:

In[8]:=
net = NetModel[ "GloVe 100-Dimensional Word Vectors Trained on Wikipedia and \ Gigaword 5 Data"]
Out[8]=

Get a list of words:

In[9]:=
words = NetExtract[net, "Input"][["Tokens"]]
Out[9]=

Obtain the vectors:

In[10]:=
vecs = Normal@NetExtract[net, "Weights"][[1 ;; -2]];

Create an association whose keys are words and whose values are vectors:

In[11]:=
word2vec = AssociationThread[words -> vecs];

Find the eight nearest words to "king":

In[12]:=
Nearest[word2vec, word2vec["king"], 8]
Out[12]=

Man is to king as woman is to:

In[13]:=
Nearest[word2vec, word2vec["king"] - word2vec["man"] + word2vec["woman"], 5]
Out[13]=

France is to Paris as Germany is to:

In[14]:=
Nearest[word2vec, word2vec["paris"] - word2vec["france"] + word2vec["germany"], 5]
Out[14]=

Net information

Inspect the number of parameters of all arrays in the net:

In[15]:=
NetInformation[ NetModel["GloVe 100-Dimensional Word Vectors Trained on Wikipedia \ and Gigaword 5 Data"], "ArraysElementCounts"]
Out[15]=

Obtain the total number of parameters:

In[16]:=
NetInformation[ NetModel["GloVe 100-Dimensional Word Vectors Trained on Wikipedia \ and Gigaword 5 Data"], "ArraysTotalElementCount"]
Out[16]=

Obtain the layer type counts:

In[17]:=
NetInformation[ NetModel["GloVe 100-Dimensional Word Vectors Trained on Wikipedia \ and Gigaword 5 Data"], "LayerTypeCounts"]
Out[17]=

Export to MXNet

Export the net into a format that can be opened in MXNet:

In[18]:=
jsonPath = Export[FileNameJoin[{$TemporaryDirectory, "net.json"}], NetModel["GloVe 100-Dimensional Word Vectors Trained on Wikipedia \ and Gigaword 5 Data"], "MXNet"]
Out[18]=

Export also creates a net.params file containing parameters:

In[19]:=
paramPath = FileNameJoin[{DirectoryName[jsonPath], "net.params"}]
Out[19]=

Get the size of the parameter file:

In[20]:=
FileByteCount[paramPath]
Out[20]=

The size is similar to the byte count of the resource object:

In[21]:=
ResourceObject[ "GloVe 100-Dimensional Word Vectors Trained on Wikipedia and \ Gigaword 5 Data"]["ByteCount"]
Out[21]=

Represent the MXNet net as a graph:

In[22]:=
Import[jsonPath, {"MXNet", "NodeGraphPlot"}]
Out[22]=

Requirements

Wolfram Language 11.1 (March 2017) or above

Resource History

  • Date Created: 2 February 2017

Reference