GloVe 300-Dimensional Word Vectors Trained on Common Crawl 840B

Represent words as vectors

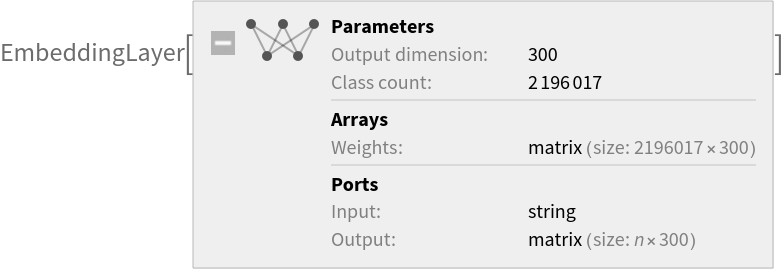
Released in 2014 by the computer science department at Stanford University, this representation is trained using an original method called Global Vectors (GloVe). It encodes 2,196,016 tokens as unique vectors, with all tokens outside the vocabulary encoded as the zero-vector. Token case is ignored.

Number of layers: 1 | Parameter count: 658,805,100 | Trained size: 3 GB |

Training Set Information

Web data from Common Crawl, trained on 840 billion tokens, with around 2.2 million unique tokens, taking into account the case.

Examples

Download Example Notebook

Open in Wolfram Cloud

Resource retrieval

Get the pre-trained net:

In[1]:=

$NetModel["GloVe 300-Dimensional Word Vectors Trained on Common Crawl \ 840B"]$

Out[1]=

Basic usage

Use the net to obtain a list of word vectors:

In[2]:=

$vectors = NetModel["GloVe 300-Dimensional Word Vectors Trained on Common Crawl \ 840B"]["hello world"]$

Out[2]=

Obtain the dimensions of the vectors:

In[3]:=

Out[3]=

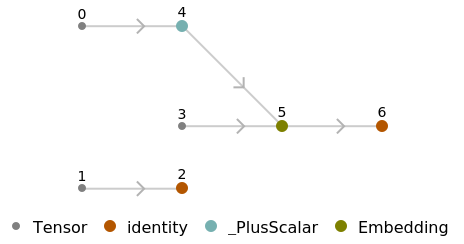
Use the embedding layer inside a NetChain:

In[4]:=

$chain = NetChain[{NetModel[ "GloVe 300-Dimensional Word Vectors Trained on Common Crawl \ 840B"], LongShortTermMemoryLayer[10]}]$

Out[4]=

Feature visualization

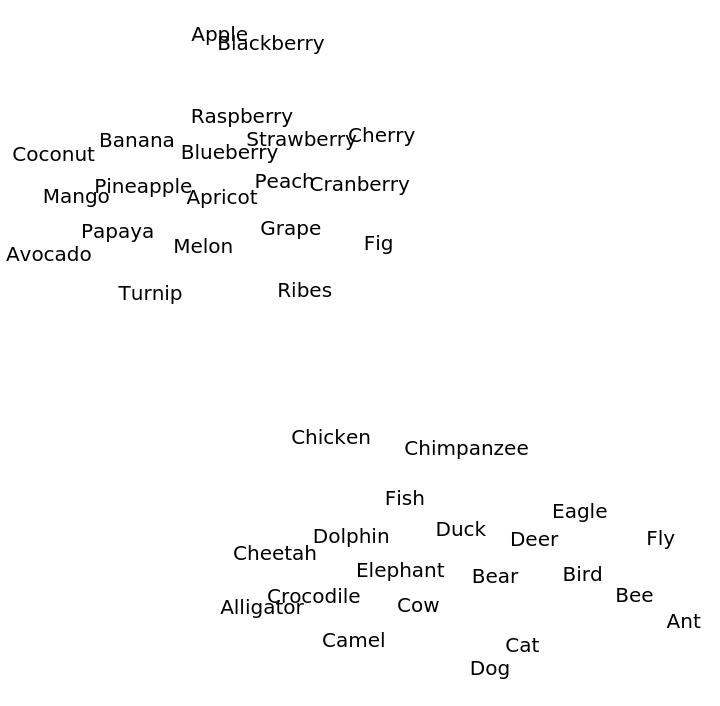
Create two lists of related words:

In[5]:=

animals = {"Alligator", "Ant", "Bear", "Bee", "Bird", "Camel", "Cat", "Cheetah", "Chicken", "Chimpanzee", "Cow", "Crocodile", "Deer", "Dog", "Dolphin", "Duck", "Eagle", "Elephant", "Fish", "Fly"};

In[6]:=

fruits = {"Apple", "Apricot", "Avocado", "Banana", "Blackberry", "Blueberry", "Cherry", "Coconut", "Cranberry", "Grape", "Turnip", "Mango", "Melon", "Papaya", "Peach", "Pineapple", "Raspberry", "Strawberry", "Ribes", "Fig"};

Visualize relationships between the words using the net as a feature extractor:

In[7]:=

$FeatureSpacePlot[Join[animals, fruits], FeatureExtractor -> NetModel["GloVe 300-Dimensional Word Vectors Trained on Common \ Crawl 840B"]]$

Out[7]=

Word analogies

Get the pre-trained net:

In[8]:=

Out[8]=

Get a list of words:

In[9]:=

Out[9]=

Obtain the vectors:

In[10]:=

Create an association whose keys are words and whose values are vectors:

In[11]:=

Find the eight nearest words to "king":

In[12]:=

Out[12]=

Man is to king as woman is to:

In[13]:=

Out[13]=

France is to Paris as Germany is to:

In[14]:=

Out[14]=

Net information

Inspect the number of parameters of all arrays in the net:

In[15]:=

$NetInformation[ NetModel["GloVe 300-Dimensional Word Vectors Trained on Common Crawl \ 840B"], "ArraysElementCounts"]$

Out[15]=

Obtain the total number of parameters:

In[16]:=

$NetInformation[ NetModel["GloVe 300-Dimensional Word Vectors Trained on Common Crawl \ 840B"], "ArraysTotalElementCount"]$

Out[16]=

Obtain the layer type counts:

In[17]:=

$NetInformation[ NetModel["GloVe 300-Dimensional Word Vectors Trained on Common Crawl \ 840B"], "LayerTypeCounts"]$

Out[17]=

Export to MXNet

Export the net into a format that can be opened in MXNet:

In[18]:=

$jsonPath = Export[FileNameJoin[{$TemporaryDirectory, "net.json"}], NetModel["GloVe 300-Dimensional Word Vectors Trained on Common \ Crawl 840B"], "MXNet"]$

Out[18]=

Export also creates a net.params file containing parameters:

In[19]:=

Out[19]=

Get the size of the parameter file:

In[20]:=

Out[20]=

The size is similar to the byte count of the resource object:

In[21]:=

$ResourceObject[ "GloVe 300-Dimensional Word Vectors Trained on Common Crawl \ 840B"]["ByteCount"]$

Out[21]=

Represent the MXNet net as a graph:

In[22]:=

Out[22]=

Construction Notebook

Download Construction Notebook

Open in Wolfram Cloud

Requirements

Wolfram Language 11.2 (September 2017) or above

Resource History

Date Created: 26 September 2017

Reference

J. Pennington, R. Socher, C. D. Manning, "GloVe: Global Vectors for Word Representation," Empirical Methods in Natural Language Processing (EMNLP), 1,532-1,543 (2014)
Available from: http://nlp.stanford.edu/projects/glove
Rights: Public Domain Dedication and License v1.0